Лекция № 12. Гидродинамические модели реакторов. Вывод характеристических уравнений.

Ранее мы рассмотрели основные модели химических процессов и их математическое описание. Усложним модель химико-технологического процесса за счет учета гидродинамических процессов, то есть способов направленного движения потоков реакционной смеси в реакторе.

Любой реактор, используемый в химическом производстве. В большем или меньшем приближении можно описать одной из следующих моделей:

• реактор идеального смешения периодического действия РИС-П;
• реактор идеального смешения непрерывного действия РИС-Н;
• реактор идеального вытеснения непрерывного действия РИВ-Н;
• каскад   реакторов   идеального   смешения   непрерывного  действия  К-РИС-Н (ячеечная модель).

Для каждой модели выведено характеристическое уравнение, которое выражает зависимость времени пребывания реагентов в реакторе о, начальной концентрации реагента, величины конверсии и скорости химической реакции.

τ = f (CA0, αA, rA)

Это уравнение является математическим описанием модели реактора. Оно дает возможность, задав СА0 (состав исходной смеси) и rA (тип химической реакции, температуру, давление, катализатор и т.п.) рассчитать время пребывания реагентов в реакторе, необходимое  для достижения заданной конверсии (αA), а значит, и объем реактора, его габаритные размеры и производительность.  Сравнивая полученные значения для реакторов разного типа, можно выбрать самый оптимальный вариант для проведения данной химической реакции.

Основанием для вывода характеристического уравнения является материальный баланс реактора, составленный по одному их компонентов реакционной смеси.

Реактор идеального смешения периодического действия

РИС-П представляет собой аппарат с мешалкой, в который периодически загружают исходные реагенты и также периодически выгружают продукты.

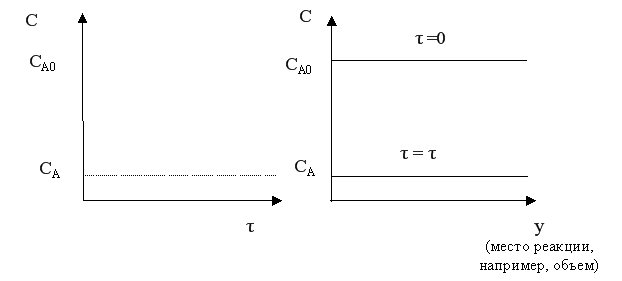
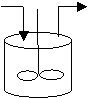В таком реакторе создается такое интенсивное перемешивание, что в каждый момент времени концентрация реагентов одинакова по всему объему реактора и изменяется лишь во времени, по мере протекания химической реакции.

Исходным уравнением для получения характеристического уравнения является уравнение материального баланса в дифференциальной форме:

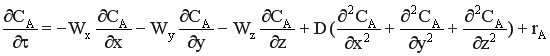
Так как вследствие интенсивного перемешивания все параметры одинаковы по всему объему реактора, в любой момент времени производная любого порядка от концентрации по осям x,y,z равна нулю.

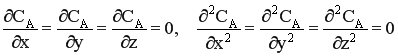
Тогда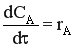               

При    Vреакци.смеси = const          CA = CA0 (1-αА).

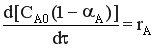
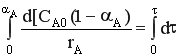
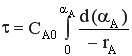   - характеристическое уравнение РИС-П

Если в реакторе протекает простая необратимая реакция «n»-го порядка, то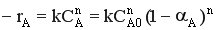 

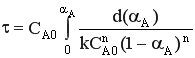
При n = 0          ,

        n = 1           .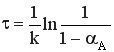

При n ≠ 0 и 1 определение τ производят методом графического интегрирования. Для этого строят графическую зависимость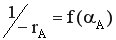

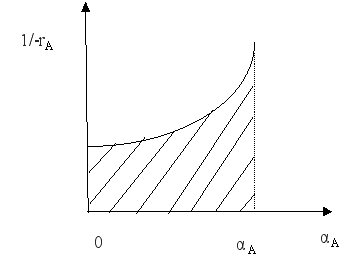
вычисляют площадь под кривой между начальным и конечным значением степени превращения.

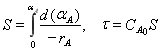
Реактор идеального вытеснения непрерывного действия

РИВ-Н представляет собой трубчатый аппарат, в котором отношение длины трубы к ее диаметру достаточно велико L/d > 20.

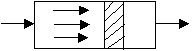
В реактор непрерывно подаются исходные реагенты, которые превращаются в продукты реакции по мере перемещения их по длине реактора.  Любая частица потока движется прямолинейно и равномерно, не происходит ни продольного, ни поперечного перемешивания. Такой режим движения реагентов называется поршневым.

Концентрация исходного реагента А постепенно меняется по длине или высоте реактора от начального значения СА0 до конечного значения СА. Следствием такого режима движения реакционной смеси является то, что время пребывания каждой частицы в реакторе одно и то же.

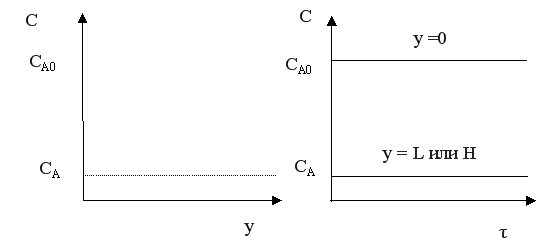
Исходным уравнением для вывода характеристического уравнения является материальный баланс в дифференциальной форме. Модель РИВ-Н предполагает движение реакционной смеси только в одном направлении – по х – координате, поэтому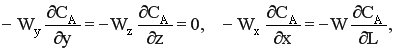  

где W – линейная скорость движения реакционной смеси, L – длина реактора.

В РИВ-Н отсутствует продольное и радиальное перемешивание, нет продольной и радиальной конвективной диффузии, а молекулярной диффузией можно пренебречь, поэтому .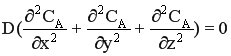

После упрощения получаем

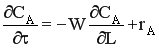- характеристическое уравнение РИВ-Н в нестационарном режиме.

При стационарном режиме 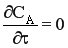(нет  накопления вещества).

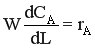
Линейная скорость движения реакционной смеси в реакторе с постоянной площадью сечения в любой момент времени равна

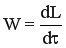,   следовательно, .

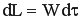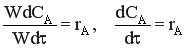
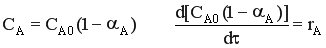
Разделим переменные и возьмем интегралы

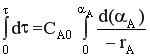
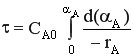- характеристическое уравнение РИВ-Н в стационарном режиме.

Реактор идеального смешения непрерывного действия

РИС-П представляет собой аппарат с мешалкой, в который непрерывно подают реагенты и также непрерывно выводят из него продукты.

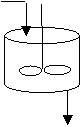В таком реакторе создается интенсивное перемешивание, поэтому по всему реактора мгновенно устанавливается одинаковая концентрация реагента, равная концентрации на выходе. Резкое (скачкообразное) изменение концентрации происходит за счет мгновенного смешения поступающих реагентов с реакционной массой, уже находящейся в реакторе.

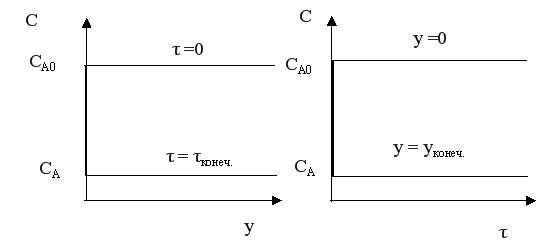
Величина перепада между начальной и конечной концентрацией зависит при прочих равных условиях от величины скорости химической реакции и от времени пребывания реакционной смеси в реакторе. Чем выше скорость и больше время, тем больше скачок концентрации.

Для РИС-Н характерно отсутствие градиентов параметров как во времени, так и по объему реактора, поэтому для вывода характеристического уравнения используют уравнение материального баланса в общей форме.

νА накопл. =  νА конвек. -  νА хим.р.

При стационарном режиме  νА накопл. =  0.

νA конвек. = νА приход – νА сток

νА приход = νА0 = CА0 vоб., где  vоб. – объемная скорость подачи реагента.

νА сток = νА0 (1-αА) = CА0 vоб. (1-αА)

νA конвек. = CА0 vоб. - CА0 vоб. (1-αА) = CА0 vоб.αА.

νA хим. =(-rA) Vp,  где Vp – объем реактора.

CА0 vоб.αА = =(-rA) Vp,               Vp = vоб τ

CА0 vоб.αА  =(-rA) vоб τ

CА0αА = (-rA) τ

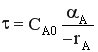- характеристическое уравнение для РИС-Н.

Для простой необратимой реакции «n»-го порядка

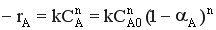
При  n = 0 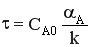  ,  при n = 1  .

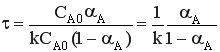Сравнение РИС и РИВ

Характеристические уравнения для РИС-П и РИВ-Н одинаковы, и время достижения заданной степени превращения реагента в этих реакторах одно и то же. Но в РИС-П полное время процесса складывается из рабочего времени, рассчитываемого по характеристическому уравнению, и вспомогательного времени на загрузку и выгрузку. В РИВ-Н вспомогательных операций нет, поэтому интенсивность РИВ-Н выше, чем в РИС-П.

В РИС-Н вспомогательных операций тоже нет, но гидродинамическая обстановка в нем отличается от обстановки в РИВ-Н, поэтому для достижения одной и той же степени превращения реагента при прочих равных условиях  требуется большее время, чем в случае РИВ-Н.

Сравним концентрационные режимы в РИС-Н и РИВ-Н. В РИВ-Н наблюдается постепенное  уменьшение концентрации реагента по длине реактора, а в РИС-Н – резкое падение концентрации до конечного значения.

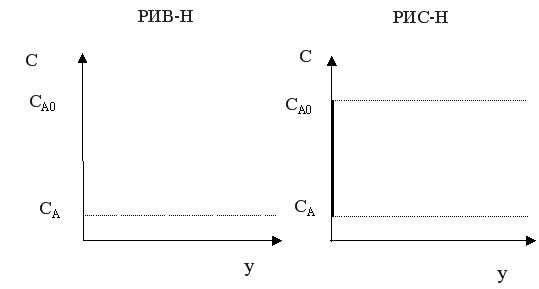
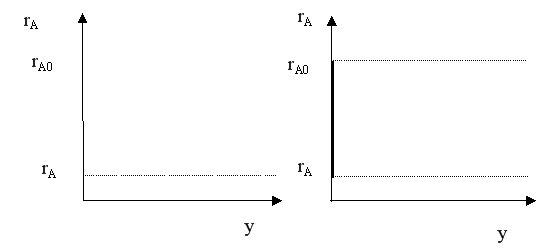
Такой же характер для этих реакторов имеет изменение скорости реакции. Следовательно, средняя скорость реакции в РИС-Н всегда ниже, чем в РИВ.

Сравним характеристические уравнения реакторов в случае реакций разного порядка.

При n = 0  характеристическое уравнение  РИС-Н и РИВ-Н имеет вид 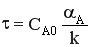. Следовательно, время, необходимое для достижения заданной конверсии реагента одинаково;   тип реактора в этом случае не оказывает влияния на интенсивность процесса. Это связано с тем, что при n = 0  скорость реакции не зависит от концентрации реагента.

При n > 0   тип реактора будет оказывать сильное влияние на интенсивность процесса.

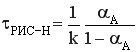
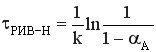
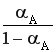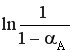>,            т.е. .

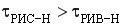Неравенство тем значительнее, чем больше конверсия реагента.

Для  сложных процессов об эффективности судят не только по размерам реактора, но и по величине селективности. Для процессов, селективность которых зависит от концентрации реагента (порядок целевой реакции ≠ порядку побочной реакции), на селективность можно повлиять, правильно выбрав тип реактора. Например, для сложно-параллельного процесса, в котором порядок целевой реакции выше порядка побочной реакции, для обеспечения высокой селективности необходимо поддерживать высокую концентрацию реагента. В этом случае лучше выбрать РИВ-Н. Если порядок целевой реакции меньше порядка побочной, нужно поддерживать низкую концентрацию реагента, поэтому более предпочтителен РИС-Н.

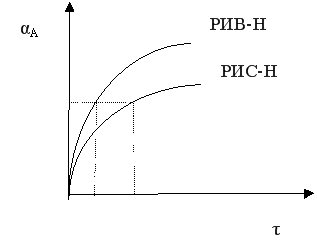
От типа реактора зависит  и выход целевого продукта. Для сложно-параллельного необратимого процесса выход можно связать с селективностью следующими соотношениями:

    РИС-Н      β = S αA;                                   РИВ-Н    .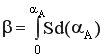

При увеличении αA

S уменьшается, если  nцел.р. > nпобоч.р.;      S увеличивается, если nцел.р. < nпобоч.р..

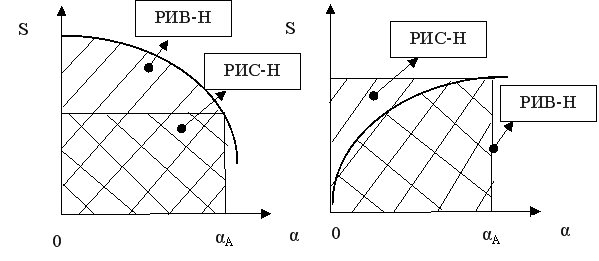
                    βРИВ-Н  > βРИС-Н                                     βРИС-Н > βРИВ-Н