Лекция № 13. Каскад реакторов идеального смешения непрерывного действия

В единичном РИС-Н нельзя добиться высокой степени превращения, так как концентрация исходного регента мгновенно падает, и весь процесс протекает при низкой скорости. Однако при проведении реакций, в которых участвуют два и более реагентов, перемешивание участников реакции является необходимым условием ее осуществления. В этом случае можно использовать реакторы, которые описывают ячеечной моделью или моделью К-РИС-Н. Каскад представляет собой несколько последовательно соединенных проточных реакторов идеального смешения.

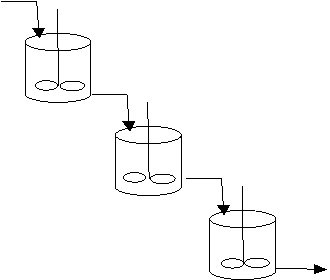
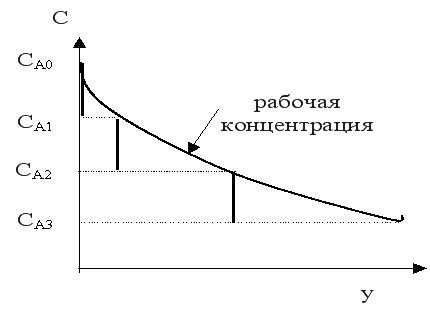
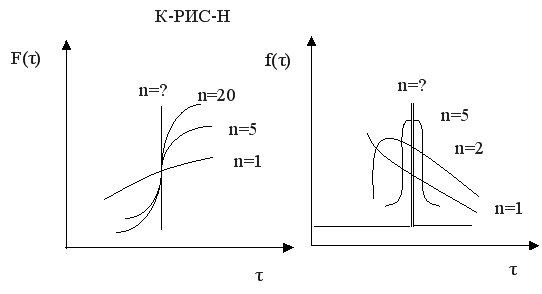
Концентрация исходного реагента в такой системе снижается до конечного значения не сразу, а постепенно от реактора к реактору. В каждом реакторе концентрация реагента в объеме постоянна и равна концентрации его на выходе из реактора; изменение концентрации происходит скачком. Однако рабочая концентрация в каскаде поддерживается выше, чем в единичном РИС-Н и при увеличении числа реакторов приближается к значению концентрации в РИВ. При  n= 8 – 10,  К-РИС-Н ≡ РИВ-Н.

Расчет К-РИС-Н сводится к расчету числа ступеней «n», необходимого для достижения заданной степени превращения реагента. Существуют графический и аналитический методы расчета каскада реакторов.

Графический метод расчета К-РИС-Н

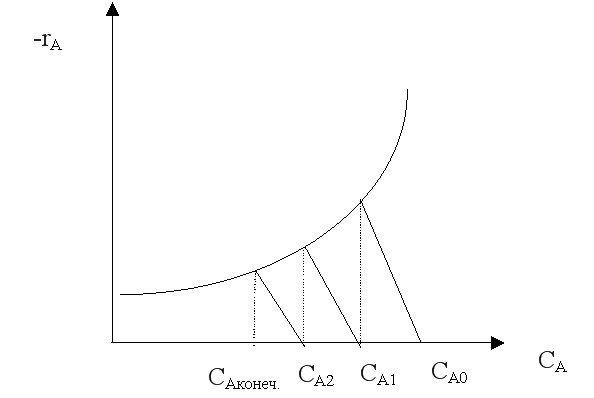
Пусть в каскаде реакторов  протекает простая  необратимая реакция  nA-го порядка. Скорость этой реакции можно описать уравнением 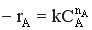 ; зависимость –rA = f (CA) представляет собой кривую.

Выведем зависимость –rA = f (CA) для единичного реактора каскада.

РИС-Н  имеет характеристическое уравнение вида    .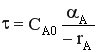

    CА = СА0 (1-αА)         CА = СА0 - СА0 αА            СА0 αА = СА0 - CА

                                           .

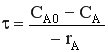
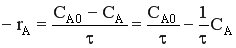
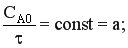
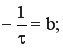
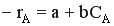Таким образом, зависимость скорости от концентрации для каждого реактора в каскаде представляет собой прямую с углом наклона, тангенс которого равен –1/τ.

Точка пересечения кривой 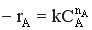и прямой 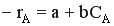характеризуют концентрацию реагента в реакторе.

Для графического расчета К-РИС-Н необходимо:

1. построить кривую ;
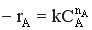2. из точки СА0 провести прямую с тангенсом угла наклона –1/τ1, где τ1 – время нахождения реагента в первом реакторе (задается);
3. из точки пересечения кривой и прямой опустить перпендикуляр на ось «х». Полученное значение СА1 есть концентрация реагента на выходе из первого реактора и на входе во второй реактор;
4. для нахождения концентрации реагента на выходе из второго реактора операцию повторить;
5. операции повторять до тех пор, пока не будет достигнута конечная концентрация реагента СА конеч., соответствующая заданной конверсии реагента.

Число повторенных операций построения прямой равно числу реакторов в каскаде.

Чаще всего, время нахождения реагента в отдельных реакторах каскада принимается одинаковым, то есть строятся параллельные прямые с одинаковым тангенсом угла наклона. Но графический метод можно использовать и при разных значениях τ, то есть при разных объеме отдельных реакторов каскада.

Аналитический метод расчета К-РИС-Н

Возможности аналитического метода ограничены сложностью получаемых уравнений, поэтому он используется в самых простых случаях.

Пусть в каскаде реакторов протекает простая необратимая реакция первого порядка.

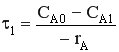                 -rA τ1 = CA0 – CA1               -rA = k CA1

k CA1 τ1 = CA0 – CA1      k CA1 τ1 + CA1 =  CA0        CA1(1+k τ1) = CA0

       →      

       →       

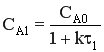
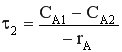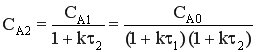
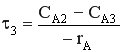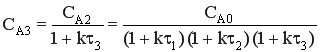
Если τ = const (τ1 = τ2 = τ3 = τ)

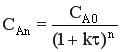
Логарифмируем полученное уравнение

                        lg CAn = lgCA0 – n lg(1+k τ)

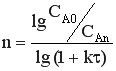
В каскаде РИС-Н концентрация реагентов изменяется ступенчато, скачкообразно от аппарата к аппарату, оставаясь постоянной в каждом из них. Высота степени (скачка) определяется скоростью реакции и размером (объемом) реактора. Чем больше объем реактора, тем больше скачок. Этим скачкообразным изменением концентрации можно воспользоваться при проведении сложных реакций. Например, если порядок целевой реакции больше порядка побочной реакции, объем реакторов в каскаде по ходу потока увеличивают, поддерживая высокую концентрацию реагента. Если порядок целевой реакции меньше, для обеспечения высокой селективности требуется поддержание низкой концентрации, поэтому объем реакторов в каскаде по ходу потока уменьшают.

Гидродинамические режимы в реальных реакторах

В реальных реакторах время достижения заданной степени превращения реагента  обычно больше, чем время, рассчитанное по характеристическим уравнениям. Это связано с тем, что в реальных реакторах гидродинамический режим отличается от идеального режима, взятого за основу при создании модели. Например, в реальном трубчатом реакторе наряду с переносом вещества в направлении движения потока реакционной массы возможно обратное движение молекул (обратная диффузия), а также перемещение вещества в радиальном направлении (радиальная диффузия).

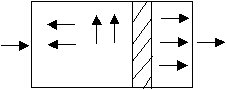
Существуют модели, учитывающие это перемещение реагентов. Модель, учитывающая только обратное перемешивание, называется однопараметрической диффузионной моделью. Модель, учитывающая наряду с обратным перемешиванием и радиальное перемешивание, называется двухпараметрической диффузионной моделью.

Для этих моделей, как и для модели РИВ-Н, справедливы равенства:

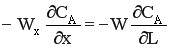
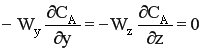
Но, в отличие от РИВ-Н, для однопараметрической модели

                          ,

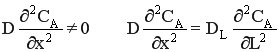где DL – коэффициент обратной диффузии.

При стационарном режиме, когда 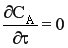, уравнение однопараметрической модели имеет вид

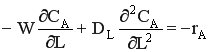
Рассуждая аналогичным образом, можно получить уравнение двухпараметрической модели

,

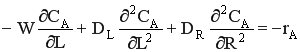где DR – коэффициент радиальной диффузии.

Степень отклонения реального реактора от идеального, которую можно количественно охарактеризовать отношением их объемов 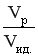, зависит от ряда показателей, например, для однопараметрической модели – от DL, линейной скорости потока W и длины реактора L. Эти показатели сведены в безразмерный комплекс 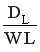, представляющий собой обратный критерий Пекле 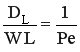.  Покажем, как изменяется показатель 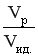при увеличении конверсии реагента при разных значениях комплекса .

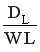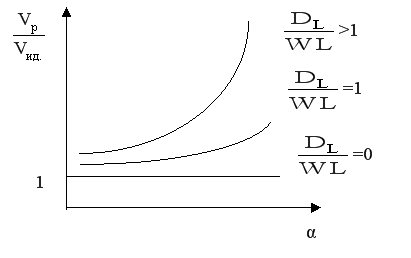
При 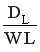 =0    Vр = Vид..

Чем больше 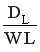, тем больше отношение  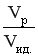, тем больше отклонение гидродинамического режима в реальном реакторе от режима в идеальном реакторе, то есть для достижения одинаковой конверсии нужен все больший объем реактора по сравнению с Vид. Особенно сильно проявляется различие при больших степенях превращения реагента.

Одно- и двухпараметрические диффузионные модели тоже не полностью описывают гидродинамический режим в реальных реакторах.

В реальных реакторах возможно образование застойных зон, где задерживается реакционная смесь, Скорость химической реакции в этих застойных зонах, если и не равна нулю, то существенно отличается от скорости реакции в основном потоке.

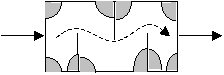
Второй причиной, по которой часть реакционного потока может не принимать участия в реакции, является наличие внутренних байпасов. Байпас – явление, при котором часть потока очень быстро проходит через реактор от входа к выходу (проскальзывает) и почти не участвует в химической реакции.

Третья причина – образование циркуляционных зон, в результате чего время пребывания частиц в реакторе становится больше.

Распределение времени пребывания в проточных реакторах

Говоря о времени пребывания реагентов в реакторе, мы имеем в виду некоторую среднюю величину. Исключение составляет лишь модель РИВ, в которой все частицы пребывают в реакторе одинаковое время. Для РИС и реальных реакторов, описываемых диффузионными и ячеечной моделями, время пребывания отдельных частиц в реакторе может быть разным. Это время зависит от траектории, которую описывает каждая частица потока в своем движении от входа к выходу. Чем сложнее эта траектория, тем большим оказывается время пребывания. В свою очередь, траектория движения частицы зависит от гидродинамики потоков (неравномерности распределения скоростей и давлений, турбулентности, внутренних течений, вызванных градиентами концентраций, температур, поверхностного натяжения и др.). Таким образом, очевидно, что для РИС и реальных реакторов время пребывания является случайной величиной и может быть описано только с помощью вычислительного аппарата математической статистики.

Непрерывная случайная величина может быть задана с помощью функций распределения случайной величины. Различают интегральную функцию распределения F(τ) и дифференциальную функцию распределения или плотность распределения f(τ).

Интегральная функция распределения – это объемная доля потока, выходящего из реактора, которая находилась в нем в течении времени, меньшим, чем τ. Свойства этой функции:

                          при τ2 > τ1     F(τ2) ≥ F(τ1)

                            F(0) = 0       F(∞) = 1

Производная от этой функции 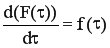называется плотностью распределения. Среднее время пребывания частицы в реакторе при использовании функций распределения можно рассматривать как математическое ожидание непрерывной случайной величины.

Экспериментально функции распределения времени пребывания могут быть найдены путем исследования так называемых кривых отклика. Суть этого метода состоит в следующем. На входе в реактор создается некоторое возмущение. Таким возмущением является введение в основной поток вещества (индикатора), отличающегося по какому-либо свойству: окраске, электропроводности, оптической плотности, кислотности, радиоактивности и т.д.). Индикатором может быть вещество, которое не изменяется и не поглощается в ходе эксперимента; концентрация его должна легко контролироваться.

Возмущение на входе (входной сигнал) может быть ступенчатым или импульсным.

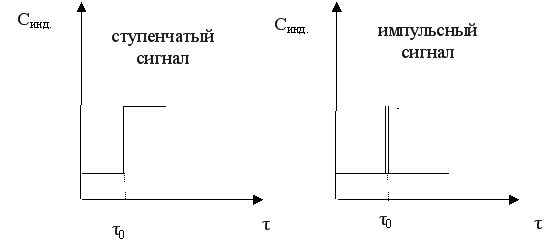
Для получения кривой отклика на входной сигнал (выходного сигнала) измеряют в разные моменты времени концентрацию индикатора в потоке, выходящим из реактора.

Синд. = f(τ)

Выходной сигнал при ступенчатом входном сигнале используют для определения интегральной функции распределения F(τ); дифференциальная функция распределения f(τ) соответствует кривой отклика на сигнал импульсной формы.

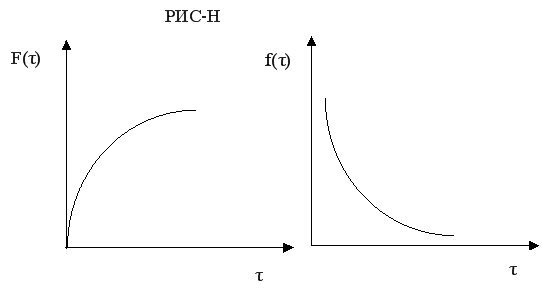
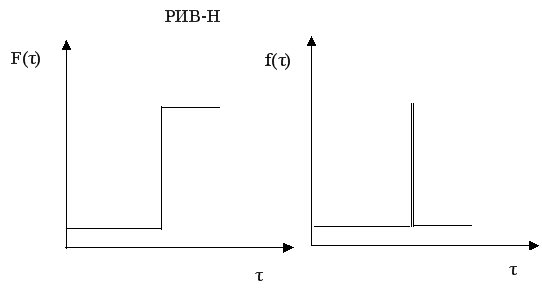
Сравним кривые отклика для идеального и реального реактора вытеснения.

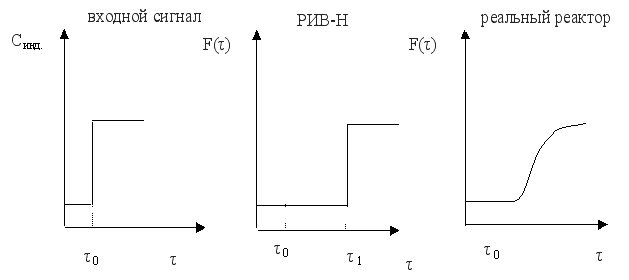
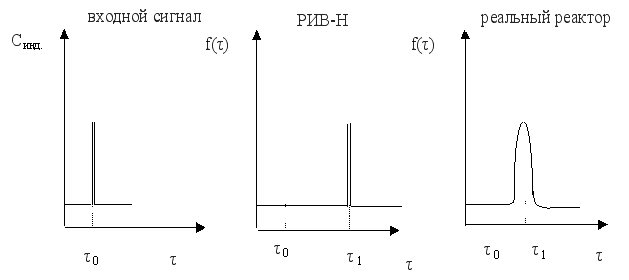
На основе функций распределения можно рассчитать среднее время пребывания частиц реагентов в проточном реакторе, определить тип модели. Учесть отклонение от этой модели и т.д.