Лекция № 14. Теплоперенос в химических реакторах

Температура оказывает существенное влияние на скорость химического процесса и другие показатели его эффективности. При проведении  реакций разного типа требуется различный температурный режим. Под температурным режимом реактора понимают поддержание в нем необходимой и оптимальной для данного процесса температуры. В промышленной практике используют два типа температурного режима:

• режим постоянных температур
• режим переменных температур.

Выбор режима определяется, в основном, технологическим классом реакции.

Температура в реакторе может изменяться по двум причинам:

1.   за счет протекания химической реакции (если реакция экзотермическая, температура повышается, если эндотермическая – понижается);
2.   за счет теплообмена с окружающей средой, то есть температура в реакторе зависит от теплового режима реактора.

По тепловому режиму выделяют три модели реакторов: адиабатический, изотермический и политропический.

Учет всех тепловых явлений осуществляется при составлении теплового баланса реактора, уравнение которого, наряду с уравнением материального баланса, является основой для расчета реакторов.

Уравнение теплового баланса реактора

В общем виде уравнение теплового баланса записывается

Qприход = Qрасход,

где  Qприход – количество тепла, поступающего в реактор в единицу времени, Qрасход – количество тепла, расходуемого в реакторе в единицу времени.

Тепло приходит в реактор с реагентами Qреаг. и выделяется (или поглощается) в результате химической реакции Qхим.р.

                   Qприход = Qреаг. ± Qхим.р.

Расход тепла происходит в результате уноса тепла с продуктами Qпрод., теплообмена с окружающей средой Qт/об.; часть тепла накапливается в реакторе Qнакоп..

                  Qрасход = Qпрод. ± Qт/об.  + Qнакоп.

           Qреаг. ± Qхим.р.= Qпрод. ± Qт/об.  + Qнакоп.

Обозначим  Qпрод.- Qреаг. = Qконв. – конвективный перенос тепла.

Тогда после преобразований получим

           Qнакоп. = - Qконв. ± Qт/об.  ± Qхим.р.  - уравнение  теплового баланса реактора в общем виде.

Если температура неодинакова в разных точках объема реактора или во времени, используют дифференциальную форму уравнения теплового баланса, выведенную для некоторого элементарного объема dx dy dz.

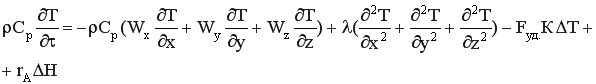
где ρ – плотность реакционной смеси; Ср – удельная теплоемкость реакционной смеси; x,y,z – пространственные координаты,  Wx, Wy, Wz - составляющие скорости движения потока в направлении осей  x,y,z; λ – коэффициент молекулярной и турбулентной теплопроводности реакционной смеси; Fуд. – удельная поверхность теплообмена; К – коэффициент теплопередачи; ∆Т = Т – Тт/нос. ( Т – температура реакционной смеси, Тт/нос. – температура теплоносителя); rA  - скорость химической реакции; ∆Н – тепловой эффект реакции.

Решение дифференциального уравнения связано с большими трудностями. Однако в каждом конкретном случае его можно упростить. Например, при стационарном режиме в проточных реакторах Qнакоп. = 0, для периодических реакторов отсутствует конвективный перенос тепла Qконв. = 0.

Выведем уравнения теплового баланса для различных гидродинамических и тепловых моделей реакторов.

1.Политропический режим

а) РИС-П

В периодическом реакторе нет конвективного переноса тепла, то есть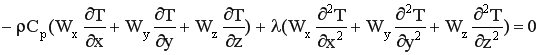       

Тогда  уравнение теплового баланса приобретает вид

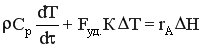
Проведем некоторые преобразования.

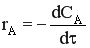            CA = CA0 (1-αA)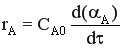            

После подстановки получим

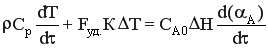
Умножив уравнение на dτ и разделив на СА0, получим

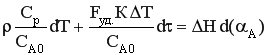
Обозначим 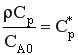   - мольная теплоемкость реакционной смеси.

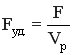, где Vp –объем реактора, F–общая поверхность теплообмена.

   СА0 Vp = NA0 – мольный расход реагента А (количество кмоль реагента А, загруженного в реактор).

Тогда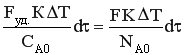        

В результате проведенных преобразований получаем уравнение теплового баланса РИС-П в политропическом режиме в следующем виде

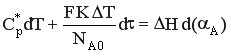
б) РИВ-Н

Тепловые процессы в РИВ-Н описываются дифференциальной формой теплового баланса при условии,  что в  реакторе не происходит накопление тепла (стационарный режим), а конвективный перенос тепла происходит исключительно по длине реактора.

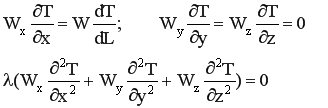
При таких условиях уравнение теплового баланса имеет вид

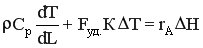
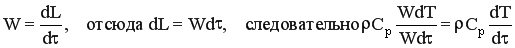
Ранее было выведено, что 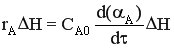  . Тогда

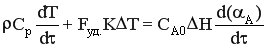
Разделим уравнение на СА0 и умножим на dτ.

                            ,

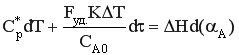где .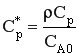

Проведем некоторые преобразования:

            ,

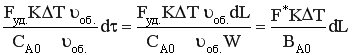где 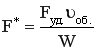  - поверхность теплообмена, приходящаяся на 1 м длины реактора, dL – длина элемента реактора, 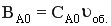- мольный расход реагента (мольная скорость, моль/час).

Итак, уравнение теплового баланса РИВ-Н в политропическом режиме имеет вид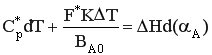                   

в) РИС-Н

Этот реактор работает в стационарном режиме, для него характерно отсутствие градиента параметров как во времени, так и по объему реактора. Поэтому уравнение теплового баланса, так же как и уравнение материального баланса, составляют сразу для всего реактора в целом.

                           Qнакопл. = -Qконвек. – Qт/об. + Qхим.р.

Qнакопл. = 0,         Qхим.р = Qконвек. + Qт/об.

Qхим.р = rA ΔH Vp = 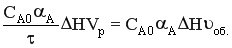, т.к. Vp = υоб.τ.

Qконвек. = ρ Ср υоб. (Т – Т0), где Т0 – температура на входе в реактор.

Qт/об. = F K ΔT.

Тогда  ρ Ср υоб. (Т – Т0) + F K ΔT = СА0 αА ΔH υоб..

Разделим уравнение на СА0 υоб. = ВА0.

Получим уравнение теплового баланса РИС-Н в политропическом режиме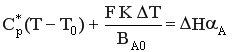                                

2. Адиабатический режим

               Qт/об. = 0

РИС-П     Ср* dT = H d(A)

РИВ-Н     Ср* dT = H d(A)

РИС-Н     Ср* (T – Т0) = H A
 

3.Изотермический режим

        T = const,    T = T0

РИВ-Н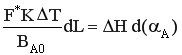     

РИС-Н      

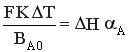
В адиабатическом режиме для РИС-Н  Ср* (T – Т0) = H A.

Отсюда       Т – Т0 = .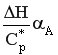

Обозначим 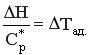- адиабатическая разность температур.

Тогда                  Т = Т0  Тад.А

Знак - соответствует эндотермической реакции, знак + - экзотермической реакции.

Такую же зависимость можно вывести для РИВ-Н в адиабатическом режиме.                Ср* dT = H d(A)

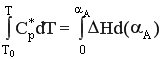
Пусть Ср* и H не зависят от температуры, тогда Ср* (T – Т0) = H A.

                            Т = Т0  Тад.А.

Это уравнение показывает, что между степенью превращения реагента и изменением температуры существует линейная зависимость. Поэтому в адиабатическом реакторе в любой момент времени (для определенной величины конверсии) можно рассчитать температуру реакционной смеси.

Устойчивость режима работы реактора

Ни один реактор не работает в строго стационарном режиме. Небольшие колебания состава исходных реагентов, температуры, давления, скорости потоков и другие возмущения могут вывести процесс из стационарного состояния. Химико-технологический процесс протекает нормально только в том случае, если малые внешние воздействия ведут к малым отклонениям от режима процесса и после снятия произведенного возмущения система может возвратиться к прежнему состоянию. Такая система называется устойчивой.

В неустойчивой системе  отклонение, вызванное случайным возмущением на входе в реактор, увеличивается во времени; режим  после снятия возмущения не возвращается в исходное стационарное состояние.

Единственной причиной неустойчивости химических процессов является температурная неустойчивость, то есть самоускорение или самозамедление реакции под воздействием изменения собственного теплового эффекта. Причина заключается в различной зависимости скорости тепловыделения  и скорости теплоотвода. При любом изменении технологического параметра происходит изменение скорости химической реакции, а значит, меняется скорость выделения или поглощения тепла. Скорость же теплоотвода или теплоподвода остается постоянной. Нарушается баланс между приходом и расходом тепла в реакторе (тепловой баланс). Следствием этого является нарушение стационарности процесса в проточном реакторе. Если произведенное нарушение режима приводит к увеличению разницы между приходом и расходом тепла, система уже не может вернуться в исходное стационарное состояние.

Условия стационарности находят при совместном решении уравнений материального и теплового балансов. Решение уравнений заключается в определении параметров процесса, при которых соблюдается равенство между приходом и расходом тепла при оптимальных показателях технологического процесса. Для этой цели часто используют графический метод.

Чтобы воспользоваться этим методом для РИВ-Н необходимо дифференциальные уравнения теплового и материального балансов, составленные для элементарного объема, проинтегрировать в пределах изменения параметров, что в большинстве случаев, представляет значительную трудность. Для РИС-Н материальный и тепловой балансы составляются в виде простых, легко решаемых уравнений. Поэтому рассмотрим графический метод определения условий стационарности на примере РИС-Н.

1. Адиабатический режим

а) Простая необратимая экзотермическая реакция   А  С,   Н  0