Проценты и процентная ставка
Процент представляет собой рентную сумму, выплачиваемую финансовым учреждениям за пользование денежными средствами.
Ставка процента или ставка роста капитала - это ставка дохода, получаемого от инвестиции.
Процентная ставка с точки зрения кредитора
| Альтернативные возможности использования собственных денежных средств |
| Потребление | Товарный обмен | Накопление | Долг | Рента |
Факторы, определяющие величину процентной ставки с точки зрения кредитора
| 1.Риск невозврата | 2.Затраты кредитора | 3.Упущенные возможности |
Процентная ставка с точки зрения должника
| Альтернативные возможности использования собственных денежных средств |
| Потребление | Товарный обмен | Накопление | Долг | Рента |
| Факторы, определяющие величину процентной ставки с точки зрения кредитора |
| Привилегия немедленного удовлетворения потребности | Ожидаемая доходность заемных средств превышает затраты на оплату процентов |
Простые и сложные проценты
Простой процент, выплачиваемый за ссуду, пропорционален продолжительности времени, на который взята ссуда
I = P*n*i
где I - выплачиваемый процент, P - сумма кредита, n - процентный срок и i - процентная ставка.
Допустим, что берется в долг 1000 по ставке простого процента 30% годовых. В конце первого года процент, подлежащий к оплате, составляет
I = 1000(1)(0.3) =300
С учетом самого долга и процентов сумма, подлежащая оплате на конец года, составит 1300.
Сложный процент - начисление процентов производится на сумму, включающую проценты, начисленные за предыдущие периоды.
n
I = P* [(1 + i) - 1]
Метод исходит из предположения, что все выплаты по процентам (процентные деньги) реинвестируются и приносят такой же процент дохода.
Допустим, что берется в долг 1000 по ставке простого процента 30% годовых на два года. Долг вместе с процентами выплачивается в конце срока кредитования. В конце первого года процент, подлежащий оплате, составляет
I = 1000(1)(0.3) = 300
а в конце второго года
I = 300 + (1000+300)*(0.3) =(1000)*[(1+0.3)^2 - 1]=[PV1] 690
Таблица 9.1
Вычисление сложного процента, когда проценты выплачиваются ежегодно
| Годы | Сумма долга на начало года (А) | Процент к оплате на конец года (В) | Сумма долга на конец года (А+В) | Сумма, оплаченная в конце года |
| 1 | 1000 | 300 | 1300 | 300 |
| 2 | 1000 | 300 | 1300 | 300 |
| 3 | 1000 | 300 | 1300 | 300 |
| 4 | 1000 | 300 | 1300 | 1300 |
Таблица 2
Вычисление сложного процента, когда проценты накапливаются
| Годы | Сумма долга на начало года (А) | Процент к оплате на конец года (В) | Сумма долга на конец года (А+В) | Сумма, оплаченная в конце года |
| 1 | 1000 | 1000SYMBOL 180 \f "Symbol" \s 10ґ0.3= 300 | 1000x1.3=1300 | 0 |
| 2 | 1300 | 1300SYMBOL 180 \f "Symbol" \s 10ґ0.3= 390 | 1000(1.3)2=1690 | 0 |
| 3 | 1690 | 1690 SYMBOL 180 \f "Symbol" \s 10ґ 0.3= 507 | 1000(1.3)3=2197 | 0 |
| 4 | 2197 | 2197 SYMBOL 180 \f "Symbol" \s 10ґ 0.3 =659.1 | 1000(1.3)4 = 2856.1 | 2856.1 |
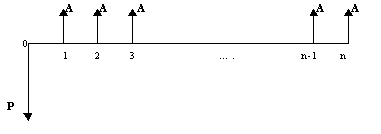
Описание денежного потока во времени
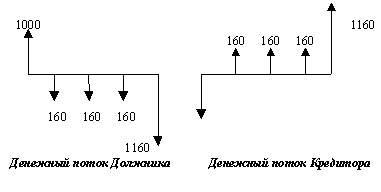
Рис. 1. Диаграмма денежных потоков
Поскольку в каждой сделке имеются два участника, направления движения денежных средств на диаграмме денежных потоков зависят от избранной точки зрения.
Чистый денежный поток представляет собой арифметическую сумму поступлений (+) и платежей (-), совершаемых одновременно.
Обозначение: Ft - чистый денежный поток в момент времени t,
Ft < 0 представляет чистый платеж денежных средств;
Ft > 0 представляет чистое поступление денежных средств.
Формулы процентов (раздельное начисление, раздельные платежи)
Допущения:
1. Окончание одного года совпадает с началом следующего года.
2. P относится к началу года, который принят как текущий.
3. F относится к концу n-го года с момента времени, принятого как текущий.
4. A производится в конце каждого года рассматриваемого периода. Когда совершаются P и A , первый A из серии совершается через год, после P. Когда совершаются F и A, последний платеж A из серии совершается одновременно с F.
1. Коэффициент сложного процента при единичном платеже
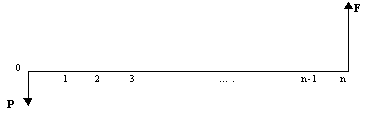
Рис. Единичная текущая сумма и единичная будущая сумма
Таблица 3.
Расчет коэффициента сложного процента при единичном платеже
| Год | Сумма на начало года | Процент в течение года | Сумма и проценты на конец года |
| 1 | P | Pi | P + Pi = P(l + i)1 |
| 2 | P(1 + i) | P(l + i)i | P(l + i) + P(l + i)i = P(l + i)2 |
| 3 | P(1 + i)2 | P(1 + i)2i | P(1 + i)2 + P(1 + i)2i = P(l + i)3 |
| n | P(1 + i)n-1 | P(1 + i)n-1i | P(1 + i)n-1 + P(1 + i)n-1i = P(l + i)n |
F = P(l + i)n
или
F = P(F/P,i,n).
ПРИМЕР:
F = 1000(F/P,30,4) = 1000(2.8561) = 2856.1
2. Коэффициент текущей стоимости при единичном платеже
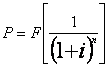
ПРИМЕР:
P = 2856.1*[1/(1 + 0.3)4] = 1811(0.3501) = 1000
3. Коэффициент накопленной суммы при серии равных платежей
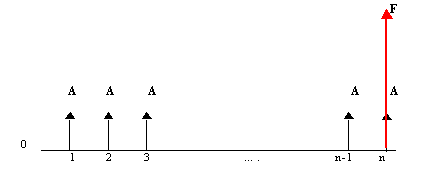
Рис. Серии равных платежей и единичная будущая сумма
Пример.
На сберегательный счет в банк ежегодно вкладывается по 100 руб. Ставка процента на сберегательном счете составляет 12 % годовых. Какая сумма будет накоплена на счете в течение 5-ти лет?
Таблица 5.
Сумма сложного процента серии ежегодных платежей
| Ко-нец года | Коэффициент сложного процента серии ежегодных платежей | Сложный процент в конце 5-го года | Общая сумма F |
| 1 | 100(1.12)4 | 157.35 | |
| 2 | 100(1.12)3 | 140.49 | |
| 3 | 100(1.12)2 | 125.44 | |
| 4 | 100(1.12)1 | 112.00 | |
| 5 | 100(1.12)0 | 100.00 | 635.28 |
F = A(1) + A(1 + i) + ...+ A(1 + i)n-2 + A(1 + i)n-1.
Умножим это выражение на (1 + i):
F(1 + i) = A(1 + i) + A(1 + i)2 + ...+ A(1 + i)n-1 + A(1 + i)n
Вычтя первое выражение из второго, получим
F(1 + i) = A(1 + i) + A(1 + i)2 + ...+ A(1 + i)n-1 + A(1 + i)n
-F = -A(1) - A(1 + i) - A(1 + i)2 - - A(1 + i)n-1
F(1 + i) -F = -A A(1 + i)n
Решение для F дает
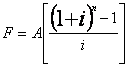
ПРИМЕР:
F = 100[(1 + 0.12)5 - 1]/0.12= 100*(6.353) = 635
4 Коэффициент аннуитета
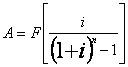
ПРИМЕР:
Tребуется накопить $635, произведя серию из пяти платежей с ежегодно начисляемым сложным процентом 12% годовых, следует каждый год совершать платеж
A = 635 * 0.12/[(1 + 0.12)5 - 1] = 635(0.1574) = 100
5. Коэффициент возврата капитала серией равных платежей
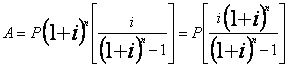
ПРИМЕР:
Инвестиционным проектом предусматривается приобретение оборудования по условиям торгового лизинга. Стоимость оборудования равна $2.000.000. Предоплата составляет 50 % от стоимости оборудования. Последующие платежи производятся ежеквартально серией равных 10 - ти платежей при ставке процента 10 % годовых. Определить сумму ежеквартальных платежей.
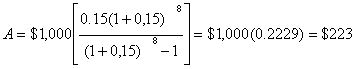
При подобной системе платежей важно определить какая часть платежа относится к возврату основного долга, а какая часть платежа является оплатой процентов по лизингу. В частности, это важно для включения процентов в себестоимость для целей налогообложения.
Схема расчета:
| N платежа | Платеж | % | Возврат тела |
| 1 | 114 259 | 25 000 | 89258 |
| 2 | 114 259 | 22 768 | 91490 |
| 3 | 114 259 | 20 481 | 93777 |
| 4 | 114 259 | 18 137 | 96121 |
| 5 | 114 259 | 15 734 | 98524 |
| 6 | 114 259 | 13 271 | 100988 |
| 7 | 114 259 | 10 746 | 103512 |
| 8 | 114 259 | 8 158 | 106100 |
| 9 | 114 259 | 5 506 | 108753 |
| 10 | 114 259 | 2 787 | 111472 |
| ВСЕГО | 1 142 590 | 142 590 | 1 000 000 |
6. Коэффициент текущей стоимости серии равных платежей
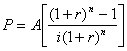
ПРИМЕР:
Текущая стоимость для серии равных платежей $223 при ставке сложного процента 15% годовых
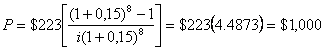
Номинальная и эффективная ставки процента
Пусть
r = номинальная годовая ставка процента;
i = эффективная ставка процента;
m = количество периодов в году.
Эффективная ставка процента на любой временной интервал:
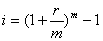
|