3.1. Статические моменты сечения
При решении практических задач возникает необходимость в использовании различных геометрических характеристик поперечных сечений бруса. Настоящий раздел посвящен методам их определения. Рассмотрим некоторое поперечное сечение в системе координат x, y (рис. 3.1) и рассмотрим два следующих интегральных выражения:
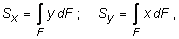 (3.1)
(3.1)
где нижний индекс у знака интеграла указывает на то, что интегрирование ведется по всей площади сечения F. Каждый из этих интегралов представляет собой сумму произведений элементарных площадок dF на расстояние до соответствующей оси (x или y). Первый интеграл называется статическим моментом сечения относительно оси x, а второй - относительно оси y.
При выполнении практических расчетов важно знать, как меняются статические моменты сечения при параллельном переносе координатных осей (рис 3.2).
Очевидно, что
x = x1 + a; y = y1 + b. (3.2)
Подставляя (3.2) в (3.1) получим:
| 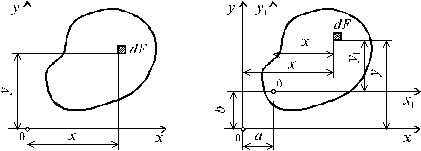 Рис. 3.1 Рис. 3.2 |
 (3.3)
(3.3)
Величины а и b можно подобрать (причем единственным образом) так, чтобы выполнялись следующие равенства:
b×F = Sx ; a×F = Sy , (3.4)
тогда статические моменты 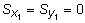 .
.
Ось, относительно которой статический момент равен нулю, называется центральной. Точка С(xC , yC) пересечения центральных осей называется центром тяжести сечения в системе координат (x, y) и определяется из (3.4):
 . (3.5)
. (3.5)
Далее предположим, что брус имеет составное сечение (рис. 3.3) с общей площадью F. Обозначим через Fk (k = 1,2,3,...,n) площадь k-ой области, принадлежащей к составному сечению бруса. Тогда выражение (3.1) можно преобразовать в следующем виде:
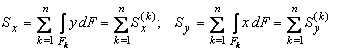 , (3.6)
, (3.6)
где 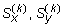 - статические моменты k-той области относительно осей x и y. Следовательно, статический момент составного сечения равен сумме статических моментов составляющих областей.
- статические моменты k-той области относительно осей x и y. Следовательно, статический момент составного сечения равен сумме статических моментов составляющих областей.
|