3.2. Моменты инерции сечения

В дополнение к статическим мо­ментам в системе координат x0y (рис. 3.1)рассмотрим три интегральных выражения:

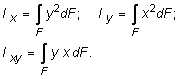(3.7)

Первые два интегральных выраже­ния называются осевыми моментами инерции относительно осей x и y, а третье - центробежным моментом инерции сечения относительно осей x, y.

Для сечений, состоящих из n-числа областей (рис. 3.3), фор­мулы (3.7) по аналогии с (3.6) будут иметь вид:

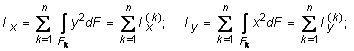
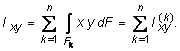
Рассмотрим, как изменяются моменты инерции сечения при параллельном переносе координатных осей x и y (см. рис. 3.2). Преобразуя формулы (3.7) с учетом выражения (3.2), получим :

(3.8)

Если предположить, что оси x₁ и y₁ (см. рис. 3.2) являются цен­тральными, тогда 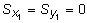и выражения (3.8) упрощаются и принимают вид:

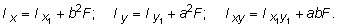(3.9)

Определим осевые моменты инерции прямоугольника относительно осей x и y, проходящих через его центр тяжести (рис. 3.4). В качестве элементарной пло­щадки dF возьмем полоску шириной b и высотой dy (рис. 3.4). Тогда будем иметь:

Аналогичным образом можно установить, что .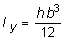

Для систем, рассматриваемых в полярной системе координат (рис. 3.5, а), вводится также полярный момент инерции:

.

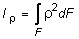где r - радиус-вектор точки тела в заданной полярной системе ко­ординат.

Рис. 3.5

Вычислим полярный момент инерции круга радиуса R. На рис. 3.5, a показана элементарная площадка, очерченная двумя ра­диусами и двумя концентрическими поверхностями, площадью

dF = rdrdj.

Интегрирование по площади заменим двойным интегрировани­ем:

.

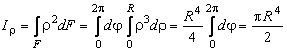Hайдем зависимость между полярным и осевыми моментами инерции для круга. Из геометрии видно (рис. 3.5, б), что

r² = x² + y²,

следовательно,

.

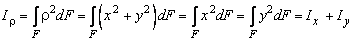Так как оси x и y для круга равнозначны, то I_x = I_y = .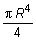

Полярный момент инерции кольца может быть найден как разность моментов инерции двух кругов: наружного (радиусом R) и внутреннего (радиусом r):

.
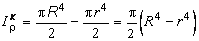