4.4. Кручение тонкостенного бруса

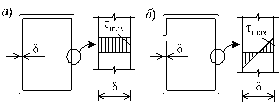
В машиностроении, авиастроении и вообще в технике широко применяются тонкостенные стержни с замкнутыми (рис. 4.7, а) и открытыми профилями (рис. 4.7, б) поперечных сечений. Поэтому расчеты на кручение таких тонкостенных стержней имеет большое практическое значение.

Характерной геометрической особенностью тонкостенных стер­жней является то, что их толщина существенно (на порядок и более) меньше других геометрических раз­меров (длиной сре­динной линии конту­ра поперечного сече­ния и длины стерж­ня).

Характер распре­деления напряжений по толщине тонкостенного стержня открытого профиля близок к равномерному (рис. 4.7, б), а замкнутого профиля меняется по ли­нейному закону, как это показано на рис. 4.7, а. Откуда следует, что напряжения в поперечных сечениях открытого профиля прак­тически не изменятся, если профиль сечения распрямить. Иначе говоря, напряжения в криволинейном открытом профиле будут примерно такими же, как и в прямом.

Обращаясь к формулам (4.14), (4.16) и при предельном пере­ходе 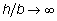, получим:

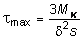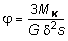; , (4.17)

где d - толщина профиля; s - длина контура профиля; l - длина стержня.

В случае, если тонкостенный незамкнутый профиль является составным (рис. 4.8) и не может быть развернут в вытянутый пря­моугольник, воспользовавшись почленной аналогией, легко опре­делить выражения напряжений на i-ом произвольном участке:

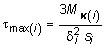, (4.18)

где M_K(i) - доля крутящего момента, соответствующего i-му участку:

,

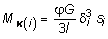где j - угловое перемещение, единое для всех участков:

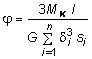. (4.19)

Изложенный подход к определению напряжений является при­ближенным, так как он не позволяет определить напряжения в зонах сопряжения элементов поперечного сечения профиля, кото­рые являются зонами концентрации напряжений.

Рис. 4.8 Рис. 4.9

Далее рассмотрим брус, имеющий поперечное сечение в форме замкнутого тонкостенного профиля (рис. 4.9). Выделим на контуре элементарный участок длиной ds и выразим крутящий момент че­рез напряжения t, выполняя операцию контурного интегрирования получим:

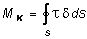. (4.20)

Из условия равновесия сил по оси z выделенного элемента дли­ной dz (4.9) легко установить, что по контуру сечения произведение t×d является постоянной величиной. С учетом данного обстоятель­ства, выражение (4.20) примет вид:

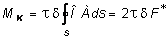, (4.21)

где 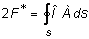- представляет собой удвоенной площадь, ограни­ченную срединной линией контура сечения.

Из (4.21) наибольшее напряжение определяется по формуле:

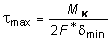. (4.22)

Для вывода выражения для угла закручивания воспользуемся энергетическими соображениями. Энергия, накопленная в элемен­тарном объеме с размерами d, dz, ds за счет деформаций чистого сдвига, равна:

.

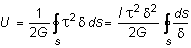С учетом (4.21), последнее выражение можно представить в виде:

.

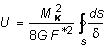С другой стороны, работу внешних сил можно представить в виде:

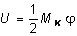. (4.24)

Приравнивая оба выражения из (4.22) и (4.23), получим:

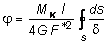, (4.25)

Если d является постоянной по контуру, будем иметь:

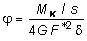, (4.26)