5.2. Основные дифференциальные соотношения теории изгиба

Пусть брус нагружен произвольным образом распределенной нагрузкой q = f (z) (рис. 5.5, а).

Рис. 5.5

Выделим из бруса элемент длиной dz и приложим по его краям положительные внутренние усилия (рис. 5.5, б). В пределах малого отрезка dz нагрузку q можно считать распределенной равномерно. Приравняем нулю сумму проекций всех сил на вертикальную ось y и сумму моментов всех сил относительно поперечной оси x, прохо­дящей через точку С (рис. 5.5, б), получим:

Q_y + qdz - Q_y - dQ_y = 0;

M_x + Q_ydz + qdz×dz/2 - M_x - dM_x = 0.

Производя упрощения и отбрасывая величины высшего поряд­ка малости, получим:

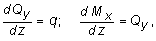(5.4)

откуда

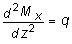. (5.5)

Из (5.4) следует, что при q = const функция Q_y будет линей­ной, а функция M_x - квадратичной. Если на каких-то участках бруса распределенная нагрузка отсутствует, т.е. q = 0, то получим, что Q_y = const, а M_x является линейной функцией от z.

В сечениях, где приложена сосредоточенная сила, эпюра Q_y претерпевает скачок на величину внешней силы. И наконец, в тех сечениях, где Q_y принимает нулевое значение и меняет знак, функция M_x достигает экстремальных значений.