5.10. Пример расчета (задача № 11)
Стальная балка АВ, расчетная схема и поперечное сечение которой показаны на рис. 5.28, а, (c = 0,03 м) нагружена силами Р1 и Р2. Требуется:
1. Построить эпюры изгибающих моментов в главных плоскостях инерции;
2. Установить по эпюрам изгибающих моментов опасное сечение балки. Найти для опасного сечения положение нулевой линии;
3. Вычислить наибольшие растягивающие и сжимающие нормальные напряжения;
4. Определить значение полного прогиба в середине пролета балки и указать его направление.
Решение
1. Построить эпюры изгибающих моментов в главных плоскостях инерции. Ввиду симметричности сечения балки относительно осей x и y (рис. 5.28, а), можно сделать вывод, что эти оси - главные. Для построения эпюр изгибающих моментов, используя принцип независимости действия сил, представим косой изгиб как изгиб в двух главных плоскостях инерции бруса (рис. 5.28, б, г). Определив опорные реакции, составим аналитические выражения изгибающих моментов и вычислим их значения в характерных сечениях. Построим эпюры изгибающих моментов Mx и My (рис. 5.28, в, г), откладывая ординаты со стороны растянутых волокон. В соответствии с принятым правилом знаков (п. 5.9), Mx < 0, My > 0.
2. Установить по эпюрам изгибающих моментов опасное сечение балки. Найти для опасного сечения положение нулевой линии. Сравнивая ординаты эпюр Mx и My, делаем вывод, что опасными могут быть сечения D или С, т.к. в них предположительно возникают наибольшие по величине изгибающие моменты. Для того, чтобы установить, какое из них является наиболее опасным, нужно вычислить возникающие в сечениях C и D наибольшие нормальные напряжения и сравнить их. Теоретически доказано, что если контур поперечного сечения так вписывается в прямоугольник, что четыре крайние точки сечения совпадают с углами прямоугольника, то максимальное нормальное напряжение будет в одном из углов прямоугольника и определится по формуле:
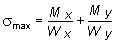 ,
,
где все величины берутся по абсолютной величине. У нас именно такой случай. Осевые моменты инерции сечения вычислим по следующим зависимостям:
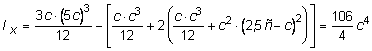 =
=
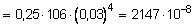 м4;
м4;
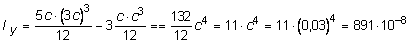 м4.
м4.
Моменты сопротивления сечения Wx и Wyопределятся следующим образом:
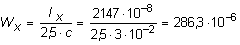 м3;
м3;
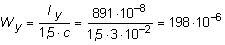 м3.
м3.
Таким образом, наибольшие напряжения в сечениях С и D равны:
сечение С
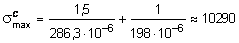 кПа = 10,29 МПа;
кПа = 10,29 МПа;
сечение D
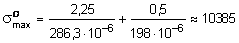 кПа = 10,38 МПа.
кПа = 10,38 МПа.
| 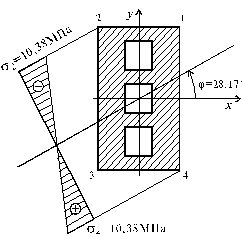 Рис. 5.29 |
Сравнивая эти значения, заключаем - опасным является сечение D. Подставив значения Ix, Iy , Mx, Myв формулу (5.29) получим:
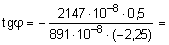
= 0,535, откуда j » 28,17°.
Нулевая линия пройдет в тех четвертях поперечного сечения, в которых изгибающие моменты будут вызывать нормальные напряжения разных знаков. В нашем случае это будут первая и третья четверти. Поэтому, отложив угол j » »28,17° от оси x против хода часовой стрелки, проведем нулевую линию (рис.5.29).
3. Вычислить наибольшие растягивающие и сжимающие нормальные напряжения. Вершины стрелок нормальных напряжений, определяемых по формуле (5.26) будут лежать на плоскости, пересекающей плоскость поперечного сечения по нулевой линии. При взгляде на плоскость напряжений вдоль нулевой линии мы увидим ее в виде прямой, ординаты которой показаны в виде эпюры s на рис. 5.29. Наибольшие нормальные напряжения будут иметь место в точках 2 и 4 и различаться только знаком. Действительно, подставляя в формулу (5.26) координаты точек 2 и 4, получаем:
точка 2
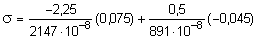 » -10385 кН/м2 »
» -10385 кН/м2 »
» -10,38 МПа;
точка 4
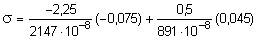 » -10385 кН/м2 »
» -10385 кН/м2 »
» 10,38МПа.
Отложив в удобном масштабе полученные величины напряжений, построим эпюру напряжений s (рис. 5.29).
4. Определить значение полного прогиба в середине пролета балки и указать его направление. Полный прогиб (перемещение центра тяжести сечения С) вычисляем по формуле:
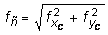 ,
,
где  - проекции полного прогиба на главные оси. Эти величины можно определить методом начальных параметров. Начало координат поместим на левом конце балки в точке А.
- проекции полного прогиба на главные оси. Эти величины можно определить методом начальных параметров. Начало координат поместим на левом конце балки в точке А.
Прогиб в плоскости x0z. Начальные параметры:
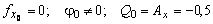 кН.
кН.
Составим выражение прогибов fx(z) с помощью универсального уравнения упругой линии балки:
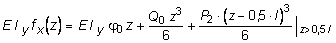 . (5.30)
. (5.30)
Величину j0 определим из условия, что при fx(l) = 0. Подставляя в выражение (5.30) z = l = 4 м, получим:
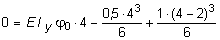 ;
;
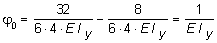 .
.
Окончательно выражение прогибов fx(z) будет иметь вид:
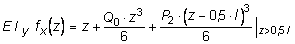 . (5.31)
. (5.31)
Для определения прогиба в середине пролета подставим z =
= 0,5×l = 2 м в выражение (5.31):
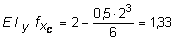 кН×м3.
кН×м3.
Учитывая, что Е = 2×108 кН/м2 и Iy = 891×10-8 м4, получаем:
 м = 7,45×10-4 м.
м = 7,45×10-4 м.
Прогиб в плоскости y0z. Начальные параметры:
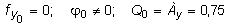 кН.
кН.
Выражение для прогибов fy(z) получаем с помощью метода начальных параметров:
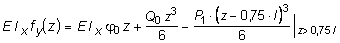 . (5.32)
. (5.32)
Подставляя z = l = 4 м в выражение (5.32) и учитывая, что в т. В прогиб равен нулю, получаем уравнение для определения j0 :
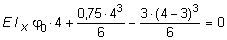 ,
,
откуда
 .
.
Окончательно выражение для прогибов fy(z) будет иметь вид:
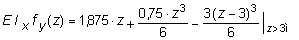 . (5.33)
. (5.33)
Для определения прогиба в середине пролета подставим z = = 0,5l = 2 м в выражение (5.33):
 кН×м3;
кН×м3;
 м = -0,64×10-4 м.
м = -0,64×10-4 м.
Определим величину модуля вектора полного прогиба
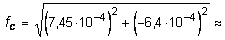
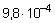 м.
м.
Направление вектора полного прогиба показано на рис. 5.30. При этом, угол b определим по формуле:
 ; b = -40,5°.
; b = -40,5°.
|