6.3. Метод сил
Суть этого метода заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и внутренних, а их действие заменяется соответствующими силами и моментами. Их величины, в дальнейшем, подбираются так, чтобы перемещения системы соответствовали тем бы ограничениям, которые на нее накладываются отброшенными связями.
Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной системы. Для каждой статически неопределимой заданной системы (рис. 6.9, а) можно подобрать, как правило, различные основные системы (рис. 6.9, б, в), однако их должно объединять следующее условие - основная система должна быть статически определимой и геометрически неизменяемой (т.е. не должна менять свою геометрию без деформаций элементов).
Рис. 6.9
Рассмотрим систему, которая дважды статически неопределима (рис. 6.10, а). Заменим в основной системе действие отброшенных связей неизвестными усилиями X1 и X2 (рис. 6.10, б). Принятая основная система будет работать также, как и заданная, если на нее наложить условие отсутствия вертикальных перемещений в точках A и B (т.е. в тех местах, где в заданной системе стоят опоры):
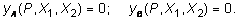 (6.9)
(6.9)
| 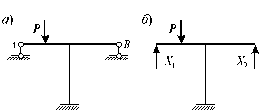 Рис. 6.10 |
Уравнения (6.9) называются уравнениями совместности деформаций и при их выполнении фактически устанавливается условие эквивалентности между заданной и основной системой при действии внешней силы Р и неизвестных усилий X1 и X2 . На основании принципа независимости действия сил (6.9) можно представить в следующем виде:
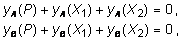 (6.10)
(6.10)
где yA(P), yB(P), yA(X1), yB(X1), yA(X2), yB(X2) - вертикальные перемещения точек А и В основной системы соответственно от действия сил Р, Х1, Х2.
Вводя обозначения d11, d12, D1P - вертикальные перемещения точки А основной системы, соответственно, от последовательного действия сил X1 = 1, X2 = 1, от внешней силы Р; d21, d22, D2P -вертикальные перемещения точки B основной системы, соответственно, от последовательного действия сил X1 = 1, X2 = 1, от внешней силы Р, и учитывая существование линейности связи между силой и перемещением, систему уравнений (6.3) можно преобразовать в канонической форме:
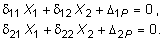 (6.11)
(6.11)
Последние уравнения носят названия канонических уравнений метода сил.
Для вычисления коэффициентов при неизвестных X1 и X2 используют формулу Мора:
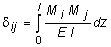 , (i,j = 1,2). (6.12)
, (i,j = 1,2). (6.12)
Легко видеть, что 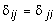 , это свойство называется законом парности коэффициентов при неизвестных. Свободные же коэффициенты определяются по формуле:
, это свойство называется законом парности коэффициентов при неизвестных. Свободные же коэффициенты определяются по формуле:
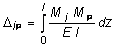 . (6.13)
. (6.13)
После решения системы (6.11) определяются величины неизвестных усилий X1 и X2 . Если их значения получились отрицательными, это означает, что реально они действуют в направлении противоположном принятому. Окончательная эпюра моментов определяется по зависимости
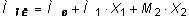 . (6.14)
. (6.14)
Эпюра поперечных сил QOK может быть построена по эпюре моментов МОК с использованием зависимости 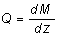 и величин приложенных к системе усилий.
и величин приложенных к системе усилий.
|