7.1. Понятие об устойчивости. Задача Эйлера
До сих пор мы рассматривали методы определения напряжений и перемещений, возникающих в стержнях и соответственно, занимались оценкой их прочности и жесткости. Однако оказывается, что соблюдение условий прочности и жесткости еще не гарантирует способности конструкций выполнять, предназначенные им функции в эксплуатационных режимах. Наряду с выполнением условий прочности и жесткости, необходимо обеспечить и устойчивость конструкций.
При неизменной схеме нагружения, под устойчивостью понимается свойство способности системы сохранять свое первоначальное равновесное состояние. Если рассматриваемая система таким свойством не обладает, то она называется неустойчивой, а ее равновесное состояние - неустойчивым состоянием.
При неизменной схеме нагружения, в процессе роста интенсивности нагрузок, явление перехода системы от одного равновесного состояния к другому равновесному состоянию, называется потерей устойчивости системы. Значения внешних сил, при которых происходит потеря устойчивости, называются критическими.
В некоторых случаях при потере устойчивости, система, переходя в новое устойчивое равновесное состояние, продолжает выполнять свои функции. Однако в подавляющем большинстве случаев, потеря устойчивости системы сопровождается возникновением больших перемещений, пластических деформаций или ее полным разрушением. Поэтому сохранение исходного (расчетного) равновесного состояния системы является важной задачей и одной из основных проблем сопротивления материалов.
| 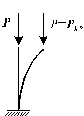 Рис. 7.1 |
Основная задача теории устойчивости заключается в определении критического значения внешних сил и ограничение их величин таким образом, чтобы исключить возможность потери устойчивости заданной системы в эксплуатационных режимах.
Пусть вертикальный стержень закреплен нижним концом, а на свободном верхнем конце центрально приложена продольная сила Р (рис. 7.1). На начальном этапе нагружения равновесное состояние системы определяется как простое продольное сжатие, так как на данном этапе нагружения в поперечных сечениях стержня, за исключением продольной силы, остальные силовые факторы равны нулю. При дальнейшем росте внешней силы Р, обнаруживается, что при некотором ее значении P = PKP, стержень изогнется. Так как явление изгиба тесно связано с действием изгибающих моментов, возникающих в поперечных сечениях стержня, можем утверждать, что при P = PKP происходила смена формы равновесного состояния системы. Если на начальном этапе нагружения P < PKP, равновесное состояние вертикального стержня определялось как простое сжатие, то при P > PKP сжатие сопровождается изгибом. Это означает, что при P = PKP происходила потеря устойчивости системы.
Заметим, что в данном случае, смена формы равновесного состояния сопровождается и сменой формы деформирования: в докритическом - прямолинейная форма деформирования, в закритическом - криволинейная, а в критическом - смешанная форма.
Заметим также, что для гибких стержней потеря устойчивости может наступить при напряжениях, значительно меньших предела прочности материалов. Поэтому расчет стержней должен выполняться при условии, что сжимающие напряжения не превышают критического значения с точки зрения потери их устойчивости:
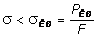 , (7.1)
, (7.1)
где РKP - значение сжимающей силы, при котором стержень переходит из прямолинейного состояния равновесия к криволинейному; F - площадь сечения стержня.
| 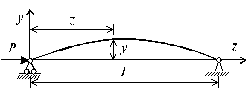 Рис. 7.2 |
Изучение устойчивости стержней начнем с простейшей задачи о стержне с двумя шарнирно опертыми концами при действии центрально сжимающей силы Р (рис. 7.2).
Впервые эта задача была поставлена и решена Л.Эйлером в середине ХVIII века и носит его имя.
Рассмотрим условия, при которых происходит переход от центрально сжатого состояния к изогнутому, т.е. становится возможной криволинейная форма оси стержня при центрально приложенной сжимающей силе Р. Предполагая, что изгиб стержня будет происходить в плоскости минимальной жесткости, записывая дифференциальное уравнение упругой линии балки и ограничиваясь рассмотрением только малых перемещений, имеем:
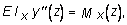 (7.2)
(7.2)
где Ix - минимальный момент инерции сечения.
Для определения выражения изгибающего момента Mx (z), действующего в поперечном сечении стержня, расположенном на расстоянии z от начала системы координат, применяя метод сечений к системе, изображенной на рис. 7.2 и рассматривая равновесие отсеченной части системы, расположенной левее от заданного сечения, получим:
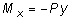 . (7.3)
. (7.3)
При положительном прогибе в выбранной системе координат знак “минус” означает, что момент является отрицательным
Введем следующее обозначение:
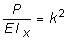 . (7.4)
. (7.4)
Тогда уравнение (7.2) преобразуется к виду:
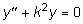 . (7.5)
. (7.5)
Решение (7.5) записывается в виде:
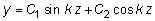 . (7.6)
. (7.6)
Постоянные С1 и С2 определяются из граничных условий задачи:
y(0) = 0; y(l) = 0.
Из первого условия вытекает, что С2 = 0, а из второго получается, что либо С1 = 0 (что нам неинтересно, т.к. в этом случае y(z) º 0), либо
sinkl = 0. (7.7)
Из (7.7) следует, что kl = pn, где n - произвольное целое число. Учитывая (7.4), получаем:
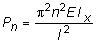 . (7.8)
. (7.8)
Это означает, что для того, чтобы центрально сжатый стержень принял криволинейную форму, необходимо, чтобы сжимающая сила была равна какому-либо значению из множества Рn по (7.8). Наименьшее из этих значений называется критической силой РKP и будет иметь место при n = 1:
РKP = 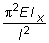 . (7.9)
. (7.9)
Эта сила носит название первой критической эйлеровой силы.
Следовательно, согласно (7.6) при Р = РKP выражение прогибов можно записать в следующем виде:
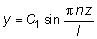 . (7.10)
. (7.10)
Из (7.10) видно, что прогибаться стержень будет по синусоиде. Графики функций прогибов y(z) при различных n изображены на рис. 7.3.
| 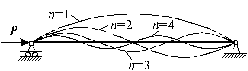 Рис. 7.3 |
Из (7.9) видно, что критическая с точки зрения устойчивости сила зависит от жесткости стержня и его длины, но никак не зависит от прочностных свойств материала стержня, т.е. два стержня одинаковой длины с идентичными граничными условиями их закрепления, изготовленных из различных материалов, но имеющих одинаковую изгибную жесткость, теряют устойчивость при одном и том же значении сжимающей силы. В этом заключается значительная разница между проверкой прочности стержня на сжатие и растяжение и проверкой на устойчивость.
При изменении условий закрепления концов стержня необходимо решение дифференциального уравнения его изгиба, но уже в виде:
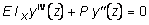 . (7.11)
. (7.11)
Анализ этих решений говорит о том, что все они могут быть представлены в следующем виде:
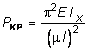 . (7.12)
. (7.12)
где m - коэффициент приведения длины. Он показывает, во сколько раз следует изменить длину шарнирно опертого стержня, чтобы критическая сила для него равнялась бы критической силе стержня длиной
l в рассматриваемых условиях закрепления. На рис. 7.4 показано несколько видов закрепления стержня и указаны соответствующие значения коэффициента m.
|