7.2. Границы применимости решения Эйлера. Формула Ясинского

Как показали опыты, решение Эйлера подтверждалось не во всех случаях. Причина состоит в том, что формула Эйлера была получена в предположении, что при любой нагрузке стержень ра­ботает в пределах упругих деформаций по закону Гука. Следова­тельно, его нельзя применять в тех ситуациях, когда напряжения превосходят предел пропорциональности. В связи с этим найдем границы применимости решения Эйлера:

Рис. 7.4

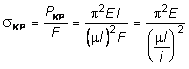, (7.13)

где 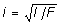- радиус инерции сечения. Если стержень имеет оди­наковые опорные закрепления в двух взаимно перпендикулярных плоскостях инерции, то при определении значения критической силы и критического напряжения, необходимо брать наименьшее значение момента инерции и, соответственно, радиуса инерции поперечного сечения.

Введем понятие гибкости стержня:

.

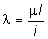Тогда (7.13) принимает вид:

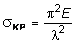. (7.14)

Из (7.14) следует, что напряжение s_КР возрастает по мере уменьшения гибкости стержня. Заметим, что стержень, имеющий неодинаковые опорные закрепления в главных плоскостях и, сле­довательно, неодинаковые приведенные длины, теряет устойчи­вость в той главной плоскости, в которой гибкость стержня имеет наибольшее значение.

Формула Эйлера неприемлема, если напряжения s_КР > s_П, где s_П - предел пропорциональности. Приравнивая (7.14) к пределу пропорциональности, получим предельное значение гибкости:

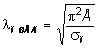. (7.15)

Если l > l_ПРЕД, то формулу Эйлера можно применять. В противном случае ею пользоваться нельзя. Для стали Ст.3 l_ПРЕД = 100.

В ситуациях, когда напряжения превышают предел пропорциональности, получение теоретического решения осложняется, т.к. зависимость между напряжениями и деформациями становится не­линейной. В связи с этим, в этих случаях пользуются эмпириче­скими зависимостями. В частности, Ф.С. Ясинский предложил сле­дующую формулу для критических по устойчивости напряжений:

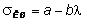, (7.16)

где a, b - постоянные, зависящие от материала, так для стали Ст.3 a = 3,1×10⁵ кН/м² , b = 11,4×10² кН/м².

При гибкостях стер­жня, находящихся в диа­пазоне 0< l< 40¸50, стер­жень настолько “коро­ток”, что его разрушение происходит по схеме сжа­тия, следовательно, кри­тические напряжения можно приравнять в этом случае к пределу пропор­циональности. Обобщая вышесказанное, зависи­мость критических на­пряжений s_КР от гибко­сти стержня l можно представить, как это сделано на рис. 7.5.