7.3. Расчет сжатых стержней на устойчивость
Как правило, основная проблема при расчете сжатых стержней состоит в том, чтобы сжимающие напряжения s не превышали бы критических значений по устойчивости sКР, т.е.
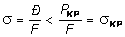 . (7.17)
. (7.17)
При продольном изгибе центрально сжатый стержень теряет несущую способность, когда напряжения в его поперечных сечениях достигают критических значений. Поэтому необходимо ввести в расчет коэффициент запаса устойчивости n по отношению к критическим напряжениям, с помощью которого и определяется допускаемое напряжение при расчете на устойчивость:
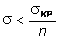 .
.
При расчете же стержней на растяжение применяют условие s < R, где R - расчетное сопротивление на растяжение.
Для унификации расчетов на растяжение и сжатие введем соотношение правых частей двух последних неравенств:
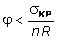 , (7.18)
, (7.18)
откуда 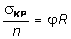 . И тогда (7.17) можно записать так: s < jR.
. И тогда (7.17) можно записать так: s < jR.
Величина j носит название коэффициента уменьшения расчетного сопротивления при расчете на сжатие и является функцией от гибкости стержня l (табл. 5).
Таким образом, окончательно формула для расчета стержней на устойчивость принимает следующий вид:
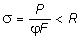 . (7.19)
. (7.19)
Несмотря на простоту выражения (7.19) расчет сжатых стержней производится, как правило, в несколько этапов. Это связано с тем, что величина j зависит от формы и размеров сечения, поэтому не может быть назначена заранее. В связи с этим, подбор сечения осуществляют итеративно, постепенно приближаясь к тому, чтобы разница между напряжением сжатия s и расчетным сопротивлением на растяжение R не превышала бы 3-5.
Таблица 5
| l | Cт 2-4 | Ст 5 | Чугун | Дерево | l | Ст2-4 | Ст 5 | Чугун | Дерево |
| 0 | 1.00 | 1.00 | 1.00 | 1.00 | 110 | 0.52 | 0.43 | - | 0.25 |
| 10 | 0.99 | 0.98 | 0.97 | 0.99 | 120 | 0.45 | 0.36 | - | 0.22 |
| 20 | 0.96 | 0.95 | 0.91 | 0.97 | 130 | 0.40 | 0.33 | - | 0.18 |
| 30 | 0.94 | 0.92 | 0.81 | 0.93 | 140 | 0.36 | 0.29 | - | 0.16 |
| 40 | 0.92 | 0.89 | 0.69 | 0.87 | 150 | 0.32 | 0.26 | - | 0.14 |
| 50 | 0.89 | 0.86 | 0.57 | 0.80 | 160 | 0.29 | 0.24 | - | 0.12 |
| 60 | 0.86 | 0.82 | 0.44 | 0.71 | 170 | 0.26 | 0.21 | - | 0.11 |
| 70 | 0.81 | 0.76 | 0.34 | 0.60 | 180 | 0.23 | 0.19 | - | 0.10 |
| 80 | 0.75 | 0.70 | 0.26 | 0.48 | 190 | 0.21 | 0.17 | - | 0.09 |
| 90 | 0.69 | 0.62 | 0.20 | 0.38 | 200 | 0.19 | 0.16 | - | 0.08 |
| 100 | 0.60 | 0.51 | 0.16 | 0.31 | | | | | |
|