7.4. Пример расчета (задача № 15)
| 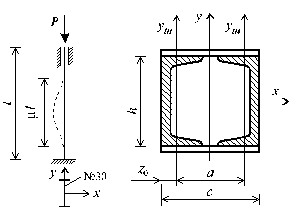 Рис. 7.6 |
Заданную стойку двутаврового (№30) поперечного сечения центрально сжатую силой Р (рис. 7.6, а), рассчитать на устойчивость, а также указать положительные и отрицательные стороны конструкции этой стойки. В целях минимизации расходов материальных ресурсов можно заменить двутавровое сечение стойки более рациональным сечением из двух швеллеров, соединенных планками на сварке (рис. 7.6, б). Подобрать сечения из двух швеллеров и сравнить результаты по площади с сечением из двутавра. Материал стоек - сталь Ст.3, расчетное сопротивление при растяжении R = 1,9×105 кПа.
Решение
1. Расчет на устойчивость стойки из двутавра. Проверка устойчивости сжатых стержней производится по формуле (7.19). Из сортамента ГОСТ 8239-72 выписываем необходимые данные для двутавра №30: F = 46,5×10-4 м2; ix = 0,123 м; iy = 0,0269 м.
Тогда из формулы (7.19) имеем:
Р = jFR. (7.20)
Для нахождения величины j нужно знать максимальную гибкость стойки, которая определится из формулы
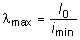 ,
,
где l0 - приведенная (свободная) длина стойки, l0 = ml. Здесь m -коэффициент приведенной длины, зависящий от способа закрепления концов стойки (для нашего примера m = 0,5), l - длина стойки; imin -минимальный радиус инерции сечения стойки (в данном случае - радиус инерции относительно оси y). Таким образом,
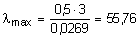 .
.
По табл. 5 находим j при l = 55,76, интерполируя до третьего знака после запятой:
при l = 50 j = 0,89;
при l = 60 j = 0,86.
Поэтому при l = 55,76
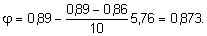
Подставляя значения F, j и R в формулу (7.20), получим допустимое значение сжимающей силы с точки зрения устойчивости рассматриваемой стойки:
Р = 0,873×46,5×10-4×1,9×105 = 771 кН.
Преимуществом стойки из двутавра является простота конструкции и малая трудоемкость изготовления и монтажа, недостатком - неравная устойчивость в разных плоскостях.
2. Подбор сечения стойки из двух швеллеров. При рассмотрении этого вопроса составное сечение стойки следует рассматривать как цельное, и поэтому расчет приведенной гибкости можно не выполнять. Подбор составного сечения стойки будем производить путем последовательного приближения. Для этого задаемся произвольным значением j, подбираем сечение и сопоставляем возникающие в нем напряжения с расчетным сопротивлением. Эта операция производится до тех пор, пока напряжение, возникающее в стойке, будет достаточно близким к расчетному сопротивлению (отклонение не должно превышать ± 5).
Примем j = 0,6. Из (7.20) определим требуемую площадь F сечения двух швеллеров:
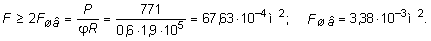
По ГОСТ 8240-72 принимаем швеллер № 24а, для которого
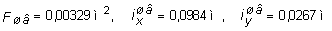 .
.
Для обеспечения равноустойчивости стойки из двух швеллеров нужно, чтобы гибкость ее была примерно одинаковой в обеих плоскостях. Для принятого сечения из двух швеллеров определим максимальную гибкость:
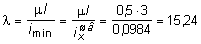 .
.
По табл. 5 находим значение j для полученной гибкости:
при l = 10 j = 0,99;
при l = 20 j = 0,97.
Для l = 15,24:
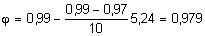 ; F = 2Fшв= 0,00658 м2.
; F = 2Fшв= 0,00658 м2.
Определяем напряжение в стойке:
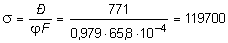 кПа £ R.
кПа £ R.
Недонапряжение составляет
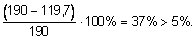
Необходимо уменьшить сечение стойки. Принимаем стойку из швеллеров № 20 (Fшв = 0,00234 м2; ix = 0,0807 м). Определим гибкость:
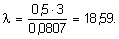
По табл. 5 для l = 18,59 находим: j = 0,973, и учитывая, что F = 2Fшв = 0,00468 м2, получим:
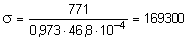 кПа £ R.
кПа £ R.
Недонапряжение составляет
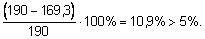
Принимаем стойку из швеллеров №18 (F = 0,00207 м2; ix =
= 0,0724 м), гибкость которой принимает значение:
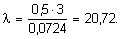
По табл. 5 для l = 20,72 находим: j = 0,973; F = 0,0414 м2:
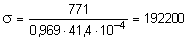 кПа.
кПа.
Перенапряжение составляет
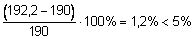 ,что допустимо.
,что допустимо.
Окончательно принимаем стойку из двух швеллеров №18. Из сортамента ГОСТ 8240-72 выписываем необходимые данные:
Ix = 1090×10-8 м4, Iy=86×10-8 м4, z0 =0,0194 м, h=0,18 м, b =0,07м.
Момент инерции поперечного сечения стойки из двух швеллеров относительно оси x: 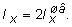 Момент инерции составного сечения относительно оси y можно изменять, сближая или удаляя швеллеры один относительно другого. Определим расстояние между швеллерами из условия, что Iy = 1,2×Ix . Из рис. 7.6, б имеем с = а +2×z0 ,где а - расстояние между собственными осями y каждого из швеллеров. Тогда:
Момент инерции составного сечения относительно оси y можно изменять, сближая или удаляя швеллеры один относительно другого. Определим расстояние между швеллерами из условия, что Iy = 1,2×Ix . Из рис. 7.6, б имеем с = а +2×z0 ,где а - расстояние между собственными осями y каждого из швеллеров. Тогда:
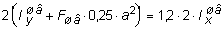 ,
,
отсюда
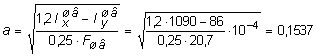 м.
м.
Монтажное расстояние между швеллерами будет с = а + 2×z0 = = 0,1537 + 2×0,0194 = 0,1925 м, принимаем c = 0,192 м. Сравнивая сечение из двух швеллеров с заданным двутавровым, видим, что площадь заданного сечения составляет 46,5×10-4 м2, а полученного из двух швеллеров - 41,4×10-4 м2. Таким образом, расход металла на стойку из двух швеллеров (без учета металла на соединительные планки) будет меньше в 46,5/ 41,4 = 1,12 раза, или на 12, чем на стойку из одного двутавра.
Однако конструкция стойки из двух швеллеров трудоемка в изготовлении по сравнению со стойкой из двутавра. Экономическое преимущество подобранного сечения стойки, состоящего из двух швеллеров, по сравнению с двутавром, объясняется более рациональным распределением ее изгибных жесткостей в различных направлениях. Это приводит к выравниванию значений моментов инерции относительно главных центральных осей инерции сечения и тем самым, к равноустойчивости стойки в указанных направлениях.
Это положение является важным обстоятельством для разработки оптимальных конструктивных решений с позиции устойчивости.
|