8.2. Колебания системы с одной степенью свободы
Рассмотрим систему, изображенную на рис. 8.2. Пренебрегая массой и продольными деформациями консольного бруса, рассмотрим колебания массы m, закрепленной на свободном конце бруса, при действии силы Р(t), изменяющейся по гармоничному закону по времени t :
Р(t) = Р0×sinwt, (8.1)
| 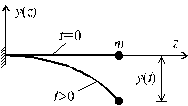 Рис. 8.2 |
где Р0 - амплитуда или максимальное значение силы Р(t), а w -круговая частота ее изменения.
При составлении уравнения движения массы m введем в рассмот-рение силу инерции PИН =-m 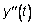 , силу сопротивления РC=-a
, силу сопротивления РC=-a 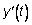 , всегда направленную против движения системы (где a -коэффициент затухания) и внешнюю силу Р(t). Перемещение y(t) в любой момент времени можно определить из уравнения:
, всегда направленную против движения системы (где a -коэффициент затухания) и внешнюю силу Р(t). Перемещение y(t) в любой момент времени можно определить из уравнения:
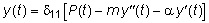 . (8.2)
. (8.2)
где d11 - перемещение массы m по вертикали под действием вертикальной единичной силы.
Отметим, что природа сил сопротивления может быть результатом сопротивления внешней среды или внутреннего трения, возникающего в частицах материала конструкции при деформации системы. Принимаем обозначения:
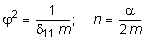 , (8.3)
, (8.3)
где j - частота собственных колебаний конструкции, n - коэффициент затухания. Тогда уравнения движения (8.2) принимает следующий вид:
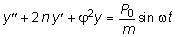 . (8.4)
. (8.4)
Решение (8.4) при начальных условиях t = 0, y = y0, 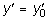 , с учетом n < j, принимает вид:
, с учетом n < j, принимает вид:
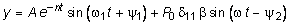 . (8.5)
. (8.5)
Здесь приняты следующие обозначения:
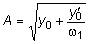 - амплитуда собственных колебаний системы;
- амплитуда собственных колебаний системы; 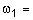
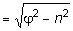 - собственная частота колебаний системы с учетом сил затухания;
- собственная частота колебаний системы с учетом сил затухания; 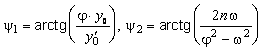 - сдвиг фазы по времени, возникающий при собственных и вынужденных колебаниях, соответственно;
- сдвиг фазы по времени, возникающий при собственных и вынужденных колебаниях, соответственно;
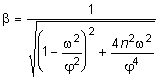 (8.6)
(8.6)
- называется коэффициентом динамичности, он показывает во сколько раз амплитуда вынужденных колебаний больше статического перемещения, вызванного максимальным значением возмущающей статической силы.
График b в зависимости от отношения частот и параметра затухания n приведен на рис. 8.3. Откуда следует, что при w ® j Р0×d11×b, т.е. амплитуда вынужденных колебаний резко возрастает, а при n ® 0, w ® j, получаем Р0×d11×b ® ¥. Это явление носит название резонанса. При n = 0 выражение для b упрощается и принимает вид:
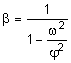 .
.
При больших t первое слагаемое из (8.5), описывающее свободные колебания системы, затухает и колебания системы описываются выражением:
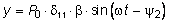 . (8.7)
. (8.7)
Заметим, что решение (8.5) при нулевых начальных условиях ( 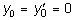 ), при любых значениях t описывается выражением (8.7).
), при любых значениях t описывается выражением (8.7).
При выполнении практических расчетов, при известном коэффициент b, легко определяется величина максимальных динамических напряжений и перемещений в упругих элементах заданной системы:
sДИН = sСТ × b; yДИН = yСТ × b;
yДИН = P0 × d11× b; yCT = P0 × d11,
где под sСТ, yCT понимается то напряжение и перемещение соответственно, которые возникали бы в системе при статическом приложении максимального значения возмущающей силы величиной P0.
Рис. 8.3
В случае, если сопоставление частот w и j указывает на их опасную близость w » j, т.е. опасность возникновения резонанса, путем конструктивных мероприятий добиваются изменения той или иной частоты. При этом, наиболее целесообразным является изменение частот в сторону увеличения отношения
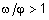
с тем условием, чтобы добиться наиболее заметного снижения коэффициента b.
|