8.4. Соударение твердого тела и системы с одной степенью свободы

Задача соударения различных механических систем часто встре­чается в инженерной деятельности в различных сферах, поэтому имеет большое практическое значение.

Взаимодействие тел, при котором за очень малый промежуток времени скачкообразно изменяются скорости взаимодействующих тел, называется ударом. В период взаимодействия соударяемых тел между ними развивается результирующая контактная сила. Хотя время действия контактной силы обычно очень мало и измеряется микро- или миллисекундами, она развивается очень быстро и принимает большие значения.

Задача соударения твердых деформируемых тел в механике, как правило, относится к классу динамических контактных задач со смешанными граничными условиями, содер­жащими в себе многие трудности математического порядка при их решении, которые не всегда могут быть преодолены простыми инженерными способами. Эти трудности в первую очередь связаны с определением с определением характера изменения функции напряжения в зоне контакта соударяемых тел по пространственным координатам и во времени. Большие сложности возникают и при учете волновых процессов, возникающих, как в зоне контакта, так и внутри соударяемых тел. Например, дифракционных волно­вых процессов по контуру в зоне контакта, и интерферен­ционных явлений внутри соударяемых тел. Здесь существенное значение приобретает и учет фактора рассеяния энергии, трудно поддающийся анализу в данном случае.

Исходя из вышеизложенного, ниже при решении задач, приме­няется упрощенный инженерный подход, основанный на следую­щих упрощающих предпосылках.

При взаимодействии соударяемых тел они принимаются или идеально упругими, или абсолютно твердыми. Деформации в упругих соударяемых телах происходят мгновенно.

С применением энергетического подхода рассмотрим соударе­ние падающего груза массой М с высоты h на систему с одной сте­пенью свободы (рис. 8.5). Считаем, что масса балки m сосредо­точена в месте соударения.

Энергетический подход является наиболее предпочтительным в тех случаях, когда требуется определить только максимальные зна­чения напряжений, динамических прогибов и не ставится задача определения законов движения заданной системы.

Составим энергетический баланс заданной системы в момент возникновения максимальных прогибов балки:

К₀ + П = U + К, (8.8)

где 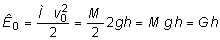- кинетическая энергия пада­ющего груза в момент соударения с балкой; П = (М + m)×g×y_max -работа внешних сил на перемещение y_max; 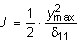- потен­циальная энергия деформации балки; К - кинетическая энергия системы при y = y_max.

Так как в состоянии наибольшего отклонения балки, y = y_max, 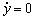, то для указанного момента времени К = 0. С учетом вышеизложенного (8.8) принимает вид:

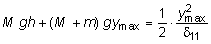, (8.9)

или

. (8.10)

Величина d₁₁ - прогиб, который получила бы балка под дейст­вием единичной статической силы, приложенной в месте удара. Следовательно, y^CТ = Mgd₁₁ представляет собой прогиб который получила бы балка под действием статически прикладываемой си­лы, равной весу падающего груза G = Mg. Тогда уравнение (8.10) можно представить в виде:

.

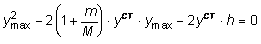Из решения последнего уравнения получаем:

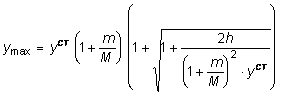. (8.11)

Отсюда, учитывая, что коэффициент динамичности определяет во сколько раз максимальный прогиб при динамическом нагру­жении больше прогиба, возникающего при статическом характере приложения нагрузки, получим:

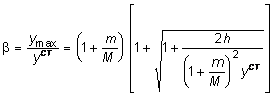. (8.12)

Величина коэффициента динамичности b, как показывает вы­ражение (8.12), зависит главным образом от жесткости рассмат­риваемой системы в направлении удара и от кинетической энергии падающего груза в момент соударения.

Для упругих систем динамические напряжения и остальные внутренние силовые факторы определяются по той же схеме, как и прогибы. Например, для напряжений, имеем:

s^ДИН = b × s^CТ . (8.13)

В тех случаях, когда масса балки m мала, по сравнению с мас­сой груза M, из (8.12), принимая m = 0, получим:

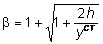. (8.14)