8.5. Пример расчета (задача № 17)

Груз G = 1,2 кН падает с высоты h = 0,12 м в точку С двутав­ровой балки КD, опирающейся на упругое сооружение, состоящее из двух балок АК и DМ (рис. 8.6, а). Сечение балки КD-двутавр №18 (I_x = 1290×10^-8 м⁴ ; W_x = 143×10^-6 м³). Сечение балок АК и DМ - двутавр №30 (I_x = 7080×10^-8 м⁴; W_x = 472×10^-6 м³). Длина ба­лок l = 1,2 м. Модуль упругости Е = 2×10⁸ кН/м².

Определить динамические напряжения в опасных сечениях ба­лок. Сравнить полученные напряжения с теми, которые появятся в балках, если балка КD будет опираться на абсолютно жесткое осно­вание.

Решение

Из уравнений равновесия балки Sm_K = 0 и Sm_D = 0 находим опорные реакции R_K , R_D :

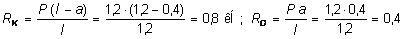кН.

Для проверки правильности найденных опорных реакций сос­тавляем уравнение равновесия Sy = 0: 0,8 + 0,4 - 1,2 = 0; 0 = 0.

Затем строим эпюры изгибающих моментов и поперечных сил для рассматриваемой балки КD и двух консольных балок АК и DМ (рис. 8.6, б, в, г, д, е).

1. Определение полного статического прогиба сече­ния С балки КD. С начала определим статический прогиб сече­ния С балки КD при опирании ее на абсолютно жесткое основание. Составим уравнение прогиба методом начальных параметров, при­няв начало координат в сечении К:

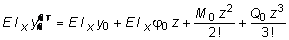. (8.15)

При этом, y₀ = 0; M₀ = 0; j₀ ¹ 0; Q₀ = R_K . Для нахождения j₀ используем условие отсутствия прогиба в сечении D y_D = 0. При
z = l м имеем:

; .

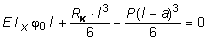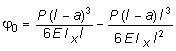Теперь, подставив найденное значение j₀ в уравнение (8.15), получим формулу для определения прогиба сечения С:

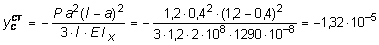м.

Для определения полного прогиба сечения С с учетом упругого характера опирания балки КD (рис. 8.6, ж) необходимо предварительно найти прогибы концов консольных балок АК и DМ. Для этого воспользуемся фор­мулой, полученной в задаче № 16:

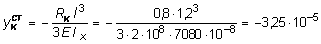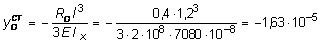м;

м.

Эпюра перемещений для составной конструкции из балок изо­бражена на рис. 8.6, ж. Величину полного перемещения сечения С балки с учетом перемещения его в результате смещения опор балки КD, опирающейся на консольные балки, определяем по формуле:

.

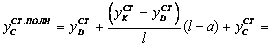
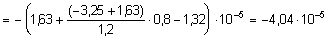Рис. 8.6

2. Определение динамических коэффициентов и на­пряжений. Динамический коэффициент при падении груза G на балку КD, опирающуюся на консольные балки АК и DМ, опреде­ляем по формуле:

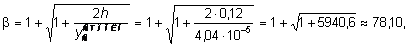
а при опирании балки КD на абсолютно жесткое основание -

.

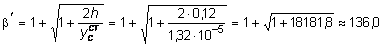Для вычисления динамических напряжений необходимо внача­ле определить статические напряжения, возникающие в сечении С:

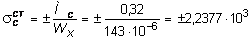кН/м²,

а затем динамические напряжения:

.

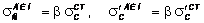Динамические напряжения, возникающие в сечении С балки КD, опирающейся на консольные балки,

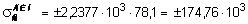кН/м²,

и динамические напряжения, возникающие в сечении С балки КD, опирающейся на абсолютно жесткое основание:

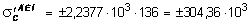кН/м².

Таким образом, если опоры лежат на абсолютно жестком осно­вание, то в сечении С возникают динамические напряжения в 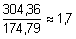раза большие по величине. Статические напряжения, возникающие в сечении А:

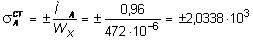кН/м².

При динамическом коэффициенте К_Д= 78,1, полученном в предположении упругого опирания балки КD в точках К и D, нахо­дим динамические напряжения в сечении А:

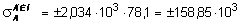кН/м².

Статическое и динамическое напряжения в сечении М балки DМ:

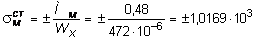кН/м².

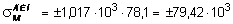кН/м².