10.2. Определение напряжений на произвольной площадке. Главные оси и главные напряжения
Из напряженного тела в окрестности произвольной точки выделим элементарный объем в виде тетраэдра (рис. 10.2).
Ориентация площадки в пространстве задается направляющими косинусами нормали v к ней - l = cos(x, v), m = cos(y, v), n =
= cos (z, v).
Вектор полного напряжения на произвольной площадке abc спроецируем на оси x, y и z. Обозначим эти проекции через 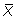 ,
, 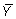 ,
, 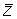 .Обозначая площадь треугольников abc, a0b, b0c, a0c через dF, dFx , dFy , dFz , соответственно будем иметь:
.Обозначая площадь треугольников abc, a0b, b0c, a0c через dF, dFx , dFy , dFz , соответственно будем иметь:
dFx = dF×l; dFy = dF×m; dFz = dF×n. (10.3)
Проецируя все силы, действующие на выделенный элемент, последовательно на оси x, y, z и с учетом (10.3) получим:
X = sx × l + tyx × m + tzx × n;
Y = tyx × l + sy × m + tzy ×n; (10.4)
Z = tzx × l + tzy × m + sz ×n.
Выразим нормальное напряжение sv на наклонной площадке через X, Y, Z:
sv = X × l + Y × m + Z × n . (10.5)
Отcюда, с учетом (10.3) получим
sv=sx×l 2 +sy×m 2 +sz×n 2 +2tyz×m×n+2tzx×n×l+2txy×l×m. (10.6)
Рассмотрим множество секущих площадок произвольной ориентации, проходящих через исследуемую точку. По нормали к каждой площадке отложим отрезок r = f(sv), координаты конца вектора которого будут следующими:
x = r × l; y = r × m; z = r × n.
Исключая из (10.6) направляющие косинусы, получим
sv×r 2 =sx×x 2+sy×y 2+sz×z 2+2tyz×yz+2txy×xy+2txz×xz. (10.7)
Принимая обозначение
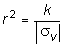 ,
,
где k - произвольная постоянная, из (10.6) получим:
sx×x 2+sy×y 2+sz×z 2+2tyz×yz+2txy×xy+2txz×xz= k. (10.8)
Из курса аналитической геометрии известно, что (10.8) представляет собой уравнение поверхности второго порядка в системе координат x, y, z. Следовательно путем поворота системы координат уравнение (10.8) можно преобразовать таким образом, чтобы попарные произведения исчезли, или иначе говоря коэффициенты попарных произведений принимали нулевые значения.
Это значит, что в произвольной точке напряженного тела существует такое положение системы координат x, y, z, в которой касательные напряжения txy, txz, tyz равны нулю.
Такие оси называются главными осями. Соответствующие им взаимно перпендикулярные площадки называются главными площадками, а нормальные напряжения на них - главными напряжениями. Принимаются такие обозначения: s1 ³ s2 ³ s3.
|  Рис. 10.2 |
Если в окрестности рассматриваемой точки определены положение главных площадок и главные напряжения, то существенно упрощается система уравнений (10.4). Они принимают вид:
X = s1 × l; Y = s2 × m;
Z = s3 × n.
Так как l 2 + m 2 + + n 2 =1, то получим:
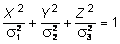 .
.
|  Рис. 10.3 |
Следовательно, геометрическое место концов вектора полного напряжения Р (X, Y, Z) образует эллипсоид, полуосям которого являются главные напряжения s1, s2, s3 (рис. 10.3). Полученный эллипсоид носит название эллипсоида напряжений. В случае равенства двух главных напряжений эллипсоид принимает форму тела вращения. Тогда каждая плоскость, проходящая через ось вращения становится главной. В случае, если все три главных напряжения равны между собой, то эллипсоид принимает форму сферы и в исследуемой точке все плоскости являются главными.
Рассмотрим как определяются величины главных напряжений через заданные значения шести компонентов напряжений s
x , s
y , s
z , t
xy , t
xz , t
yz в произвольной системе координат
x,
y,
z. Возвращаясь к рис. 10.2, предполагаем, что наклонная площадка является главной.
Обозначая полное напряжение на этой площадке через S можем записать:
X = S×l; Y = S×m; Z = S×n. (10.9)
Соотношения (10.4) преобразуются к виду:
S × l = sx × l + tyx × m + tzx × n;
S × m = tyx × l + sy × m + tzy × n; (10.10)
S × n = tzx × l + tzy × m + sz × n;
или
(sx - S) × l + tyx × m + tzx × n = 0;
tyx × l + (sy - S) × m + tzy × n = 0; (10.11)
tzx × l + tzy × m + (sz - S) × n = 0.
Так как, l 2 + m 2 + n 2 = 1, следовательно, l, m, n одновременно не могут быть равны нулю. Для того, чтобы система однородных уравнений (10.11) относительно l, m, n имела бы решение, отличное от нулевого, необходимо, чтобы определитель этой системы был равен нулю.
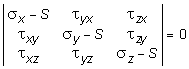 . (10.12)
. (10.12)
Отсюда
S 3 - S 2 I1 + S I2 - I3 = 0, (10.13)
где
I1 = sx + sy + sz ;
I2 = sy sz + sz sx + sx sy - tyx2 + tyz2 + txz2;
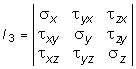 . (10.14)
. (10.14)
Все три корня уравнения (10.13) являются вещественными и определяют значения главных напряжений s1, s2, s3. Коэффициенты I1, I2, I3 называются инвариантами напряженного состояния и их значения не зависят от выбранной системы координат x, y, z.
Для определения положения главных площадок необходимо вычислить значения направляющих косинусов следующим образом. В два из трех уравнений системы (10.11) подставляются значения главных напряжений s1, s2, s3, а в качестве третьего используется равенство l 2 + m 2 + n 2 = 1.
Если I3 = 0 очевидно, что один из корней уравнения (10.7) также будет равен нулю. В этом случае напряженное состояние является плоским или двухосным. В частности, напряженное состояние чистого сдвига представляет собой двухосное напряженное состояние, для которого имеется s1 = -s3 , s2 = 0.
|  Рис. 10.4 |
Если I2 = I3 = 0 то из уравнения (10.13) очевидно, что имеет место два нулевых корня и только одно из главных напряжений отлично от нуля. Напряженное состояние в этом случае называется одноосным. Данное обстоятельство имеет место при простом сжатии или растяжении бруса или при чистом изгибе.
На практике, если имеется сложное напряженное состояние, для выполнения расчетов на прочность необходимо выразить напряжения, действующие на произвольной площадке, проходящей через данную точку, через главные напряжения. С этой целью рассмотрим равновесие призмы, показанной на рис. 10.4.
Проецируя все силы, действующие на призму, на оси, совпадающие с векторами s и t (рис. 10.4), получим:
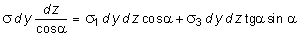 ;
;
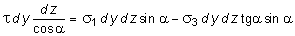 .
.
Эти выражения можно преобразовать к виду:
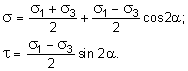 (10.15)
(10.15)
Рассматривая совместно полученные выражения для s и t, можно получить следующее выражение:
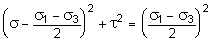 .
.
В системе координат s, t это уравнение окружности. Полученный круг называется кругом Мора или круговой диаграммой напряженного состояния. В заключение заметим, что при 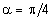 имеет место:
имеет место:
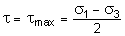 .
.
|