10.4. Физические уравнения теории упругости для изотропного тела. Обобщенный закон Гука

Для получения полной системы уравнений, описывающих на­пряженное и деформированное состояние тела, необходимо распо­лагать равенствами, связывающими напряжения и деформации. В эти равенства должны входить параметры, характеризующие физи­ческие свойства материалов. Поэтому они называются физически­ми уравнениями механики сплошной среды.

Составим аналитическое выражение обобщенного закона Гука, справедливого для идеально упругого изотропного тела. Для этого воспользуемся принципом независимости действия сил. Рассмот­рим раздельно силы, возникающие на гранях элементарного парал­лелепипеда (рис. 10.1). При малых деформациях, действие каса­тельных напряжений вызывает только формоизменение, а от дейст­вия нормальных напряжений происходит изменение линейных раз­меров выделенного элемента. Учитывая данное обстоятельство, для трех угловых деформаций получаем:

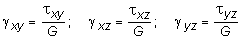, (10.18)

где G - модуль сдвига материала.

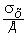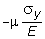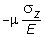Линейная деформация по оси x, обусловленная напряжением s_х, будет равна . Напряжениям s_y, s_z соответствуют дефор­мации по оси x обратного знака, равные и , соот­ветственно (здесь m - коэффициент Пуассона). Следовательно

.

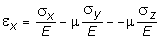Аналогично можно определить относительные удлинения ребер параллелепипеда (рис. 10.1), перпендикулярных осям y и z. Запи­сывая для e_y и e_z аналогичные уравнения окончательно получим:

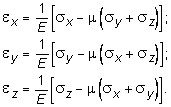(10.19)

Отсюда, получим выражение для объемной деформации

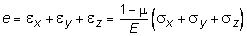. (10.20)