10.7. Плоская задача в декартовых координатах

На практике различают два вида плоской задачи - плоскую де­формацию и обобщенное плоское напряженное состояние.

В случае плоской деформации линейные деформации вдоль од­ной из координатных осей, например, оси z отсутствуют, а напря­жения имеются e_zz = 0; s_zz ¹ 0. Примером плоской деформации может служить деформация длинной стенки постоянного сечения, в случаях когда внешние нагрузки расположены в плоскостях, перпендикулярных оси z, где ось z направлена вдоль стенки.

Примером обобщенного плоского напряженного состояния мо­жет служить напряженно-деформированное состояние тонкой пла­стины, в случае, когда внешние нагрузки приложены по ее контуру и равномерно распределены по толщине пластины рис. 10.5.

Рис. 10.5

Расположим начало системы координат x, y, z в серединной плоскости пластины, а ось z направим перпендикулярно к ней, тогда будем иметь: e_zz ¹ 0; s_zz = 0.

Плоская задача теории упругости, как и объемная задача, может быть решена как в перемещениях, так и в напряжениях.

Здесь рассмотрим решение плоской задачи обобщенного на­пряженного состояния в напряжениях допуская, что объемной си­лой является собственный вес, постоянный для всех точек тела. Пусть g_y - вес единицы объема тела. В данном случае искомыми величинами являются следующие три компонента вектора напря­жений s_xx , s_yy , t_xy . Предполагая, что s_zz = 0 и все производные по оси z равны нулю, основные уравнения теории упругости значи­тельно упростятся и примут вид:

уравнения равновесия

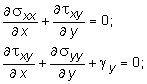(10.27)

уравнения неразрывности деформации

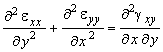; (10.28)

физические уравнения, т.е. закон Гука:

(10.29)

В результате совместного рассмотрения этих выражений полу­чим:

Ѳ (s_xx + s_yy ) = 0, (10.30)

где 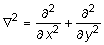- оператор Лапласа.

Следовательно, решение краевой задачи теории упругости в напряжениях, в случае обобщенного плоского напряженного сос­тояния, упрощается и сводится к решению уравнения (10.30) с учетом граничных условий, заданных на контуре тела:

,

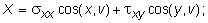
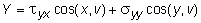где v - внешняя нормаль к площадке; X, Y - компоненты полного напряжения на границе по осям x и y.

Решение плоской задачи теории упругости значительно упро­щаются с использованием функции напряжений Эри j(x, y), вы­бранной таким образом, чтобы уравнения равновесия (10.27) пре­вращались бы в тождества, т.е.:

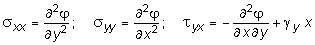. (10.31)

Подставляя первые два выражения (10.31) в (10.30) получим:

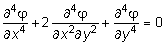. (10.32)