10.9. Пример расчета (задача № 20)
| 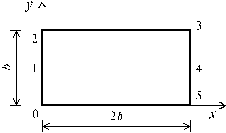 Рис. 10.6 |
Дана прямоугольная невесомая пластина (рис. 10.6), по кромкам которой действуют внешние силы, равномерно распределенные по ее толщине, равной единице. Под действием этих сил в пластине возникает обобщенное напряженное состояние, описываемое функцией напряжений в виде полинома четвертой степени
j = 2bx3 - 3x2 y2 + y4.
Требуется:
1. Проверить возможность существования такой функции напряжений;
2. По функции напряжений найти выражения компонентов напряжений;
3. Выяснить характер распределенных по кромкам пластины внешних сил, под действием которых имеет место данная система напряжений, и построить эпюры напряжений;
4. По полученным эпюрам напряжений, принимая их за эпюры распределенной внешней нагрузки, произвести проверку равновесия пластины.
Решение
1. Проверить возможность существования такой функции напряжений. Для выполнения проверки существования заданной функции напряжений выполним ее дифференцирование:
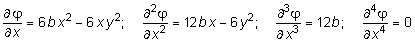 ;
;
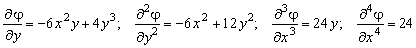 ;
;
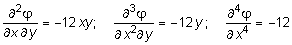 .
.
Подставив четвертые производные в бигармоническое уравнение (10.32), видим, что оно удовлетворяется: 0 + 2(-12) + 24 = 0. Следовательно, напряженное состояние пластины, выраженное зааной функцией напряжений, возможно.
2. По функции напряжений найти выражения компонентов напряжений. Компоненты напряжений, действующих по кромкам пластины, равны:
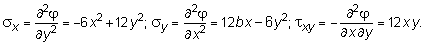
3. Выяснить характер распределенных по кромкам пластины внешних сил, под действием которых имеет место данная система напряжений, и построить эпюры напряжений. Используя функциональные компоненты напряжений в пластине, построим соответствующие эпюры напряжений по контуру пластины на каждой ее боковой стороне.
Сторона 0-1-2 (x = 0, 0 £ y £ b). На этой грани действуют напряжения sxx = 12y2 ; txy = 0:
y = 0 (точка 0) sxx = 0, txy = 0,
y = b/2 (точка 1) sxx = 3b2, txy = 0,
y = b (точка 2) sxx = 12b2, txy = 0.
Сторона 2-3 (0 £ x £ 2b, y = b). На этой грани действуют напряжения syy = 12bx - 6b2; txy = 12bx:
x = 0 (точка 2) syy = -6b2, txy = 0,
x = 2b (точка 3) syy = 18b2, txy = 24b2.
Сторона 3-4-5 (x = 2b, 0 £ y £ b). На этой грани действуют напряжения sxx = -24b2 + 12 y2; txy = 24by:
y = 0 (точка 5) sxx = -24b2, txy = 0,
y = b/2 (точка 4) sxx = -21b2, txy = 12b2,
y = b (точка 3) sxx = -12b2, txy = 24b2.
Сторона 0-5 (0 £ x £ 2b, y = 0). На этой грани действуют напряжения syy = 12bx; txy = 0:
x = 0 (точка 0) syy = 0, txy = 0,
x = 2b (точка 5) syy = 24b2, txy = 0.
По полученным результатам строим эпюры sxx, syy и txy , которые приведены на рис. 10.7.
Рис. 10.7
4. По полученным эпюрам напряжений, принимая их за эпюры распределенной внешней нагрузки, произвести проверку равновесия пластины. Выполним проверку равновесия пластины. Для этой цели найдем равнодействующие внешних сил, действующих по кромкам пластины (рис. 10.8):
Подсчет значений равнодействующих сил (рис. 10.8):


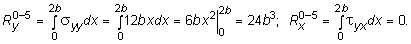
Далее определяются статические моменты площадей эпюры нормальных напряжений, действующих по кромкам пластины, относительно координатных осей x и y, с целью вычисления координат точек приложения равнодействующих сил от нормальных напряжений:
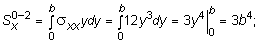

Расстояния от точек действия результирующих нормальных сил до соответствующих координатных осей принимают следующие значения (рис. 10.8):
Рис. 10.8
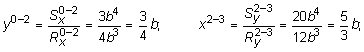
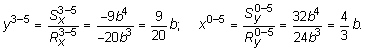
В заключении, проверим условия нахождения пластины в равновесном состоянии:

Уравнения равновесия удовлетворяются, следовательно, пластина находится в равновесном состоянии.
|