11.4. Пример расчета (задача №23)
Для толстостенной стальной трубы, имеющей внутренний диаметр d = 0,03 м и наружный диаметр D = 0,18 м, и изготовленной из пластичного материала с sT = 250 МПа и с коэффициентом Пуассона m = 0,5, требуется:
1. Определить давление pT, при котором в материале трубы начнется пластическое деформирование;
2. Определить предельное внутреннее давление pПР , при котором весь материал будет находиться в пластическом состоянии;
3. Построить эпюры распределения напряжений sr , sj , sz по толщине стенки для двух состояний трубы, рассмотрены в п. 1 и 2;
4. Определить допускаемое значение давления pa = pДОП при коэффициенте запаса прочности n = 1,5.
Решение
1. По формуле (11.32) определяем давление, при котором на внутренней поверхности трубы появятся пластические деформации:
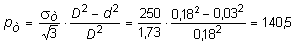 МПа.
МПа.
2. С учетом того, что pa = pT , из (11.28) определяем напряжения, соответствующие началу пластического течения:
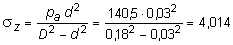 МПа;
МПа;
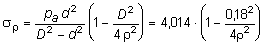 ;
;
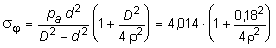 .
.
Данные для числовых расчетов сводим в табл. 6.
Таблица 6
| r×10-2, м | sj | sr |
| 1,5 | 148,5 | -140,5 |
| 3 | 40,1 | -32 |
| 6 | 13,0 | -5,0 |
| 9,5 | 8,0 | 0 |
Эпюры напряжений sr , sj , sz для упругого состояния материала трубы приведены на рис. 11.9, а.
Рассмотрим теперь предельное состояние трубы, когда весь материал трубы находится в пластическом состоянии. Предельное давление в этом случае определяется по формуле pПР 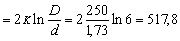 МПа.
МПа.
Рис. 11.9
3. Для определения напряжений sr , sj , sz воспользуемся формулами (11.36), (11.37), (11.38):
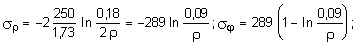
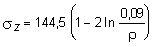 .
.
Данные для числовых расчетов сводим в табл. 7
Таблица 7
| r×10-2, м | sr | sj | sz |
| 1,5 | -517,8 | -228,9 | -373,4 |
| 3 | -317,6 | -28,6 | -173,1 |
| 6 | -117,5 | -171,7 | 27,2 |
| 9 | 0 | 289,0 | 144,5 |
Для более точного построения эпюр sj и sz определим точки, в которых указанные напряжения равны нулю:
для эпюры sj
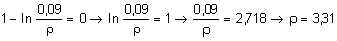 ×10-2 м.
×10-2 м.
для эпюры sz
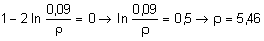 ×10-2 м.
×10-2 м.
4. Эпюры напряжений sr , sj , sz приведены на рис. 11.9, б. Допускаемое значение внутреннего давления определяется из условия pДОП = pПР/n: pДОП = 517,8/1,5 = 345,2 МПа.
|