3.3. Понятие о степени подвижности механизма
Если в пространственной к. ц., состоящей из «n» подвижных звеньев, имеются к.п. 1-ого, 2-ого,… 5-ого класса, число которых, соответственно, p1,p2,… p5, то к. ц. имеет число степеней свободы, определяемое формулой А.П. Малышева.
W=6n-5p5-4p4-3p3-2p2-p1 (3.1)
Так как любой механизм имеет одно неподвижное звено (стойку) и «n» подвижных звеньев, то формула (3.1) может использоваться для определения W пространственного механизма, где n – число подвижных звеньев, а W – степень подвижности механизма, показывающая сколько нужно иметь ведущих звеньев (двигателей) для получения определенного движения остальных его звеньев.
Для плоского механизма степень подвижности определяется по формуле Чебышева:
W=3n-2p5-p4, (3.2)
.
При этом к.п. 5-ого класса существует в виде поступательных, вращательных и винтовых.
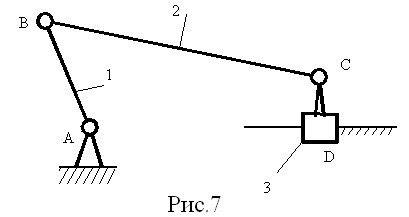
Например, кривошипно-ползунный плоский меха-низм (рис.7), в котором n=3; p5=4; p4=0,
имеет W=3·3-2·4-0=1.
При определении W необходимо учитывать возможность наличия так называемых «пассивных» звеньев, т.е. звеньев, устраняемых без формального ущерба для кинематики анализируемого механизма .
а) W=3·4-2·6-0=0 – с пассивным звеном,
б) W=3·3-2·4-0=1 – фактически.
Кроме того, необходимо учитывать возможность наличия избыточных связей, которые не реализуются в реальном механизме, а их число q определяется разностью между числом связей в к.п. действительного и формально возможного механизмов.
На рис. 9, а показан действительный механизм, а на рис. 9, б – формально возможный механизм, имеющий функциональное назначение, аналогичное действительному механизму, но где все связи, в отличие от действительного механизма, реализованы.
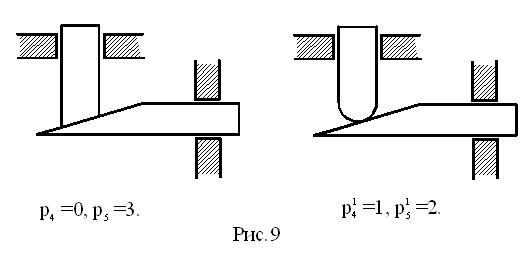
Число избыточных связей q в действительном механизме равно:
q=(2p5+p4)-(2p/5+p/4)=(2·3+0)-(2·2+1)=1,
т.е. степень подвижности действительного механизма равна:
W=3n-2p5-p4+q=3·2-2·3-0+1=1.
В общем случае пространственного механизма:
W=6n-åi·pi+q, (i от 1 до 5).
|