4.2. Определение скоростей и ускорений механизма методом планов

Метод планов является одним из самых наглядных. Определению подлежат линейные скорости и ускорения отдельных точек и угловые скорости и ускорения звеньев. При этом предварительно составляются векторные уравнения для скоростей и ускорений точек звеньев, совершающих сложное движение, например:

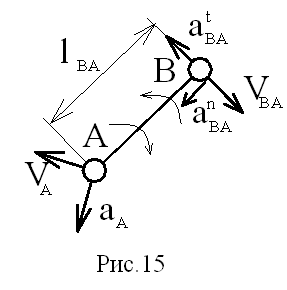а) звено совершает плоскопараллельное движение, состоящее из переносного, т.е. поступательного со скоростью полюса и относительного вращательного вокруг полюса (рис.15).

Принимая за полюс т. A, получим:

V_B=V_A+V_BA; где V_BA=w·l_AB;

a_B=a_A+a_BA; где a_BA=aⁿ_BA+a^t_BA при

aⁿ_BA=w²·l_AB; a^t_BA=e·l_AB.

Здесь V, a, w, e - линейные скорости и ускорения соответствующих характерных точек, а также угловые скорость и ускорение звена (индексы соответствуют характеру ускорений и обозначениям точек).

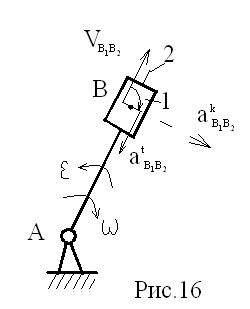б) звено совершает сложное движение, состоящее из переносного вращательного и относительного поступательного, например, звено 1 (рис.16).

Пусть B₁ и B₂ – точки, принадлежащие звеньям 1 и 2. Тогда:

V_B1=V_B2+V_B1B2, где V_B2=w·l_AB.

a_B1=a_B2+a^t_B1B2+a^k_B1B2, где ускорение Кориолиса

a^k_B1B2=2V_B1B2·w и совпадает с направлением вектора V_B1B2, повернутого на 90^○ в сторону переносного вращения.

Решение векторных уравнений осуществляется графически путем построения так называемых планов скоростей и ускорений, на которых абсолютные скорости и ускорения откладываются от одной точки, называемой полюсом, в определенном масштабе.

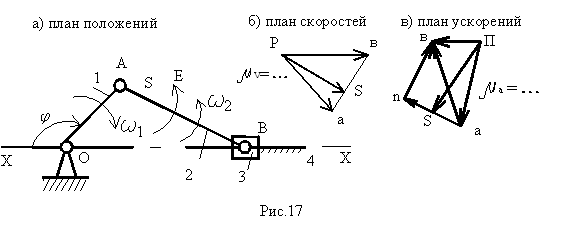
Пример расчета кривошипно-ползунного механизма рассмотрен на рис.17, где план положений (рис.17, а), план скоростей и ускорений (рис.17, б, в).

Векторные уравнения для скоростей записываются в виде:

V_B=V_A+V_BA; V_B=V_Bx+V_BBx;

где V_A=w₁·l_OA; V_Bx=0; V_BA_|_AB; V_BBx||x-x,

т.е. в выбранном масштабе μ_V: pb||x-x; ab_|_AB

V_BA= μ_V·ab; V_B= μ_V·pb и w₂= V_BA/ l_AB.

Векторные уравнения для ускорений при w₁=const записываются в виде:

a_B=a_A+a_BA; a_B=a_Bx+a^k_BBx+a^t_BBx; где a_A=aⁿ_A=w₁²·l_OA; a_BA=aⁿ_BA+a^t_BA;

здесь aⁿ_BA=w₂²·l_AB; a^t_BA=ε₂·l_AB; a_Bx=0; a^k_BBx=0; a^t_BBx||x-x.

Все ускорения представлены на рис.17 в выбранном масштабе μ_a в виде соответствующих отрезков, например, a_B=μ_a·πb и т.д.

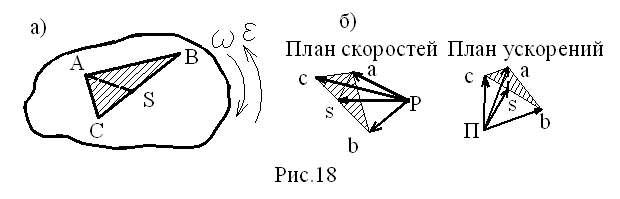
При определении скоростей и ускорений промежуточных точек звеньев, например т. S, можно использовать так называемую теорему подобия, согласно которой точки на плане положений звеньев и соответственные точки на планах скоростей и ускорений образуют подобные фигуры или пропорциональные отрезки. Рассмотрим доказательство данной теоремы. На рис.18 показано звено ABC и планы скоростей и ускорений для точек этого звена:

отрезок ca на плане скоростей соответствует V_CA_|_CA;

отрезок ca на плане скоростей соответствует V_CA_|_CA;

отрезок ab на плане скоростей соответствует V_AB_|_AB;

отрезок bc на плане скоростей соответствует V_BC_|_BC;

т.е. треугольник abc подобен треугольнику ABC.

Ускорения относительного (вращательного) движения равны:

; ; ,

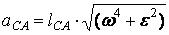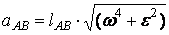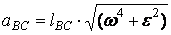т.е. a_CA/ l_CA =a_AB/ l_AB =a_BC/ l_BC или ca/CA=ab/AB=bc/BC,

Следовательно, треугольник abc подобен треугольнику ABC. Аналогичным является построение фигур для любой промежуточной точки, например т. S (рис.18, а, б).