4.4. Кинематическое исследование рычажных механизмованалитическим методом

Аналитические методы исследования позволяют проводить анализ с заданной степенью точности. Кроме того, создание математических моделей механизмов позволяет решать задачи их оптимального синтеза при использовании ЭВМ.

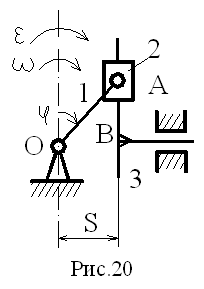Рассмотрим пример кинематического исследования синусного механизма (механизм двойного ползуна), где кривошип 1 вращается с угловой скоростью ω и угловым ускорением ε (рис.20).

Тогда скорость и ускорение точки А равны:

V_A=l_OA·ω; .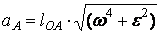

Все точки звена 1 и 2 описывают окружности, а точки звена 3 движутся поступательно, имея перемещения, скорости и ускорения равные:

S_B=l_OA·sinφ=l_OA·sinωt; V_B=dS_B/dt=dS_B·dφ/dφ·dt=l_OA·ω·cosφ;

a_B=d²S_B/dt=l_OA·(ε·cosφ-ω²·sinφ)

при ε=0 a_B=-l_OA·ω²·sinφ.

При исследовании многих механизмов получаются достаточно громоздкие формулы, что не является препятствием при использовании ЭВМ.

При исследовании пространственных механизмов используются элементы векторной алгебры и векторного анализа. Положения, скорости и ускорения точек механизма выражаются в векторной форме, при необходимости вычисляются проекции на оси и плоскости. Примеры таких исследований изложены в учебной литературе.