5.3. Уравнение движения машины

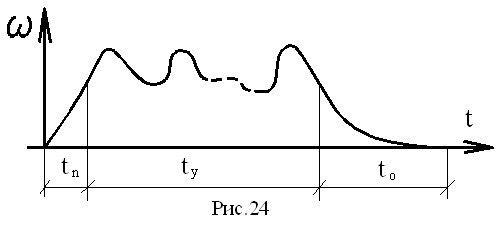
Работу машины можно разбить на 3 периода:

1) период пуска (разгон);

2) период установившегося движения;

3) период остановки (выбега);

Аналитическая зависимость между действующими на звенья силами и кинематическими параметрами движения называется уравнением движения. Это уравнение в общем случае имеет вид ∆Т=А_д-А_с, где ∆Т=Т-Т₀ – изменение кинетической энергии за рассматриваемый промежуток времени (Т и Т₀ – величина кинетической энергии в конце и начале промежутка);

А_д-А_с – суммарная работа действующих сил за рассматриваемый промежуток (А_д, А_с – работа движущих сил и сил сопротивления).

В период пуска А_д-А_с=∆Т>0, т.е. происходит ускорение движения звеньев, являющегося неустановившемся.

В период установившегося движения А_д-А_с=∆Т=0, т.е. скорости звеньев в конечный и начальный моменты цикла равны и вся работа движущихся сил расходуется на преодоление сопротивлений.

В период остановки А_д-А_с=∆Т<0, движение продолжается некоторое время за счет накопленной кинетической энергии, поглощаемой за счет сопротивления движению.

Уравнение движения может быть выражено в интегральной и дифференциальной форме, а для упрощения его решения исследование машины заменяют исследованием звена приведения, в котором изменение кинетической энергии равно: ∆T^пр =А_д^пр-А_с^пр, где суммарная работа действующих на звено приведения сил может быть выражена:

а) в интегральной форме:

А_д^пр-А_с^пр=∫F_∑^прds или А_д^пр-А_с^пр=∫M_∑^прdφ;

б) в дифференциальной форме:

dT^пр=M_∑^прdφ или M_∑^пр=dT^пр/dφ;

т.е. при dT^пр=1/2·J^пр·ω² получим:

M_∑^пр=(dJ^пр/dφ)·(ω²/2)+J^пр·ω·(dω/dφ)·(dt/dt)=(dJ^пр/dφ)·(ω²/2)+ε·J^пр.

Таким образом, уравнение движения машины приводится к тому или иному конкретному виду и решается графическим и графоаналитическим методами, а учитываемые силы и моменты сил, а также приведенные массы и моменты инерции могут быть как постоянными так и переменными величинами, зависящими от того или иного фактора.