5.4. Понятие об уравновешивающей силе. Теорема Жуковского о жестком рычаге

Одним из способов определения приведенной силы F^пр является способ, предложенный проф. Н.Е. Жуковским. Уравнение, из которого может быть найдена F^пр, основано на равенстве мощностей: F_∑^пр·V_A·cos(F_∑^пр V_A)=∑F_i·V_i·cos(F_i V_i).

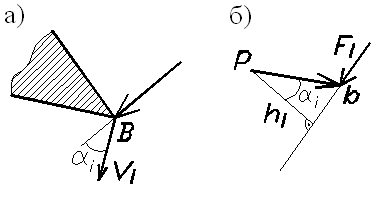
Рассмотрим какое-либо звено механизма, в т. В которого приложена сила F_i под углом α_i к вектору скорости V_i этой точки (рис.25, а).

Мощность силы F_i равна:

P_i=F_i·V_i·cosα_i.

Если вектор скорости т. В (план скоростей) повернуть на

Рис. 25 90^˚ и силу F_i приложить к концу вектора (в т. «b»), сохранив ее направление, то момент этой силы относительно полюса «p» будет равен (рис.25, б): M_i=F_i·h_i=F_i·V_i·cosα_i=P_i,

т.е. равен мощности силы F_i. Таким образом, F_i можно найти, повернув на 90^˚ план скоростей и приложив к нему все внешние силы, включая силы инерции, в соответствующих точках и сохраняя их направления. Тогда из уравнения моментов такого рычага:

F_∑^пр·h_пр=∑F_i·h_i, получим: F_∑^пр=∑F_i·h_i/h_пр, где h_i и h_пр – кратчайшие расстояния от полюса плана скоростей до линии действия i-ой и приведенной сил.

Повернутый на 90^˚ план скоростей с приложенными к нему силами называется жестким рычагом Жуковского.

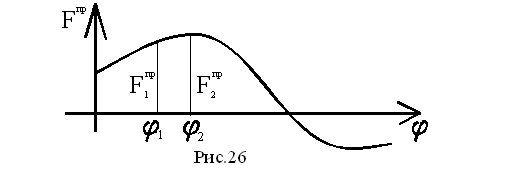
Величина F^пр или М^пр зависит от положения механизма, поэтому можно построить диаграмму, например, F^пр(φ), являющуюся функцией положения звена приведения. Для этого необходимо последовательно определить значения F^пр методом рычага Жуковского для целого ряда положений механизма в пределах цикла (F₁^пр, F₂^пр,…) и отложить их на диаграмме (рис.26).

Приведенная сила F_∑^пр или момент М_∑^пр характеризует реакцию механизма на движение его входного звена по определенному закону, задаваемому двигателем. Сила или момент, равные по величине приведенной силе или моменту, но противоположные им по направлению называется уравновешенной силой F_ур или моментом М_ур. Эта сила или момент развивается двигателем и обеспечивает заданное движение входного звена.

Если к рычагу Жуковского приложить все внешние силы, включая силы инерции, а также F_ур, то его можно рассматривать в равновесии, из условия которого: F_ур·h_ур+∑F_i·h_i=0 можно определить неизвестную F_ур, а также найти мощность двигателя P_дв, требуемую для получения заданного движения входного звена в заданном положении:

P_дв=F_ур·V_A·cos(F_урV_A)=M_ур·ω.