5.9. Силовой расчет рычажных механизмов

Зная активные силы, действующие на звенья механизма и силы инерции этих звеньев, можно произвести его кинетостатический расчет, т.е. определить реакции в кинематических парах и уравновешивающую силу (момент) на входном звене, причем эта сила (момент) является движущей при совпадении ее направления с направлением движения входного звена или силой (моментом) сопротивления, если ее направление противоположно этому движению.

При кинетостатическом расчете реакции в кинематических парах определяются путем статического расчета, который базируется на результатах кинематического анализа, включая ускорения, необходимые для определения сил (моментов) инерции.

При силовом расчете используется принцип Даламбера, позволяющий решение задачи динамики свести к статическому расчету. Согласно этому принципу приведение ускоренно движущейся системы в равновесие обеспечивается условным приложением к этой системе сил инерции. При этом неизвестные силы определяются из уравнений статики.

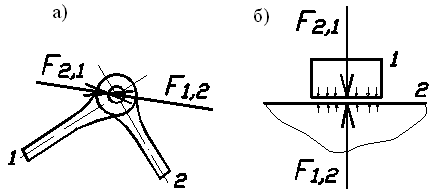
РИС. 32

Силы взаимодействия между звеньями (реак­ции) можно считать направлеными по нор-­

мали к контактирующим

поверхностям, если рас­чет ведется без учета сил тре­ния (рис.32, а, б).

При графоаналитическом решении используется метод плана сил. Механизм расчле­няется на структурные группы Ассура и начальные зве­нья. Расчет ведется, на­чиная с последней структурной группы и заканчивается рас­четом входного звена.

При расчете структурных групп к ним прикладываются все действующие силы, включая силы инерции и реакции отброшенных связей. Каждая из неиз-

вест­ных реакций, при необходимости, может быть разложена на две составляю­щие по выбранным направлениям, например, вдоль оси звена (нормаль­ная Fⁿ) и перпендикулярно оси (тангенциальная F^t). При равенстве числа уравнений статики числу неизвестных реакций их можно определить аналити­чески и графически, построив многоугольник (план) сил. Неизвестные опре­делятся из условия замкнутости векторной суммы сил. Рассмотрим при­меры:

1) Двухповодковая группа с вращательными парами:

F_i,1^t определяется из уравнения моментов для звена 1 - ∑М_B=0 относи­тельно т. В. (рис.33, а);

F_j,2^t определяется из уравнения моментов для звена 2 - ∑М_В=0 относи­тельно т. В (рис.33,а).

При отрицательных значениях реакций необходимо изменить их направле­ния на противоположные.

F_i,1ⁿ и F_j,2ⁿ определяются из плана сил (рис.33,б), полученного на основе вектор­ного уравнения;

∑F_k=0, где F_k – силы, действующие на структурную группу.

Рис. 34

2) Двухповодковая группа шатун-ползун (рис.34, а, б)

F_j,2 определяется из уравнения моментов - ∑М_А=0 относительно т. А. F_i,1=F_i,1ⁿ+F_i,1^t определяется из плана сил (рис.34,б) на основе векторного уравне­ния ∑F_k=0.

3) Двухповодковая группа кулиса-камень (рис.35, а)

F_i,1=F_i,1ⁿ+F_i,1^t определяется из плана сил (рис.35, в), на основе векторного уравне­ния ∑F_k=0.

При этом особенность расчета данной группы Ассура состоит в возмож­ности некоторого упрощения вычислений в случае, когда весом камня 2 можно пренебречь. Тогда реакция F_j,2 противоположна реакции F_1,2 и перпендику­лярна АВ, т.е. линия ее действия известна (рис.35, б).

4) Входное (начальное) звено (рис.36, а).

F_j,1=F_j,1ⁿ+F_j,1^t определяется из плана сил (рис.36,б) согласно векторному уравне­нию ∑F_k=0.