8.10. Корригирование зубчатых колёс
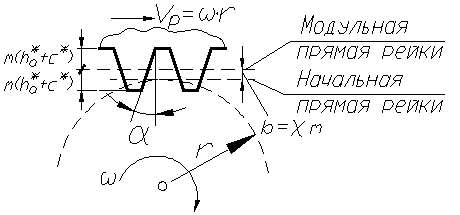При нарезании колёс режущий инструмент можно располагать ближе к заготовке или дальше от неё. Положение инструмента определяется расстоянием между делительной окружностью колеса и так называемой модульной прямой рейки, проходящей через середину высоты зуба режущего инструмента (рис.78).
рис. 78
В зависимости от положения рейки по делительной окружности может перекатываться без скольжения либо модульная прямая рейки, либо начальная прямая, отстоящая от модульной прямой на величину смещения “b”, которое называется сдвигом или коррекцией, а коэффициент χ (хи), равный χ=b/m, называется коэффициентом смещения инструмента. Если инструмент смещён от нарезаемого колеса, то χ считается положительным (положительная коррекция), а если – к центру колеса, то χ отрицателен (отрицательная коррекция). При χ=0 нарезаемое колесо называется нормальным (нулевым). Толщина зуба и ширина впадины такого колеса по делительной окружности равны.
При положительной коррекции увеличивается прочность зуба, но уменьшается длина линии зацепления, а следовательно и коэффициент перекрытия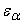 
. При отрицательной коррекции – обратный эффект, т. е. увеличивается плавность и бесшумность работы передачи, но прочность зуба уменьшается.
Зацепление двух зубчатых колёс характеризуется суммарным коэффициентом коррекции χΣ=χ1+χ2, причём возможны три случая:
1) χΣ=0 при χ1=χ2=0, когда в зацеплении находятся два нулевых зубчатых колеса (нулевое зацепление);
2) χΣ=0 при χ1=-χ2, когда в зацеплении находятся два корригированных зубчатых колеса, коэффициенты коррекции которых равны по величине и противоположны по знаку (равносмещённое зацепление с высотной коррекцией);
3) χΣ≠0, когда в зацеплении находятся два корригированных колеса, имеющих:
а) χΣ>0 – положительное неравносмещённое зацепление с угловой коррекцией;
б) χΣ<0 - отрицательное неравносмещённое зацепление с угловой коррекцией.
В первых двух случаях (χΣ=0) делительные окружности совпадают с начальными, угол зацепления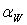 
равен углу исходного контура рейки 
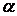и межосевое расстояние равно 
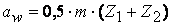, в отличие от неравносмещённого зацепления, где делительные и начальные окружности не совпадают, 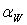≠ 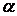, а межосевое расстояние равно: 
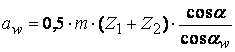, с учётом того, что
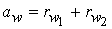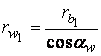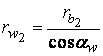при 
; 
и
; 
.
|
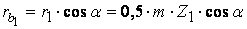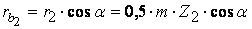