8.17.2. Методы синтеза эпициклических механизмов

Задача подбора чисел зубьев колёс для эпициклическиого механизма в общей постановке является оптимизационной ввиду множества возможных решений. Её можно считать типичной задачей дискретного нелинейного программирования, если за критерий оптимальности принять габариты или вес механизма, а ограничениями на целочисленные параметры Z₁, Z₂,… будут условия (а-д). Такую задачу можно решать различными методами, например, численными методами направленного перебора, когда варьируются Z₁, Z₂,… с целью минимизации габаритов или веса при соблюдении ограничений. Такая задача может быть решена с помощью ЭВМ.

Применяются упрощённые методы, позволяющие найти одно из конструктивно допустимых решений. Один из таких методов – метод сомножителей.

Представим числа зубьев в виде нескольких сомножителей:

; ; ; .

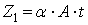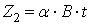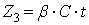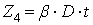Из условия (б) 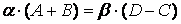. Это уравнение превращается в тождество при: ; .

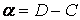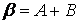Тогда: ; ;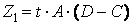

; .

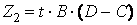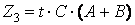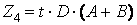Подставив эти выражения в условие (а), получим: .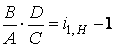

Таким образом, величину ( 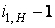) можно представить в виде нескольких сомножителей (A, B, C, D). Далее определяются значения t, обеспечивающие выполнение условий сборки и правильного зацепления и выбирается одно из этих значений. Например, из условия сборки (г)

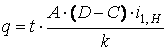
выбираются значения t, обеспечивающие целочисленность q. После этого можно определить числа зубьев.

Пример: ; .

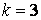Представим 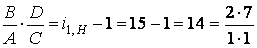, т.е. А=1; В=2; С=1; D=7. Тогда

,

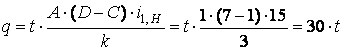следовательно условие сборки выполняется при 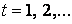Так как при :

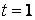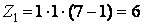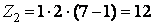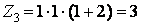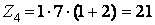; ; ; , то с учётом условий правильного зацепления, когда 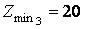, принимаем 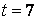. Тогда ; ; ; .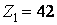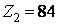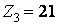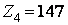