9.4. Трение качения

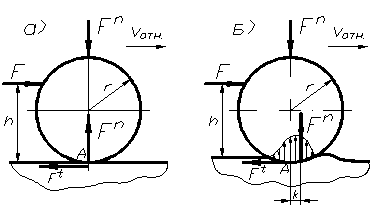
В случаях идеально твёрдых тел, одно из которых катится по поверхности другого, соприкосновение их происходит по линии или в точке и сопротивление качению отсутствует, так как линии действия сил 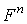совпадают (рис. 94, а) и сумма моментов относительно точки А равна 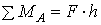. В действительности соприкосновение происходит не по линии, а по поверхности вследствие деформаций (рис. 94, б) и сумма моментов ( 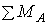) равна:

.

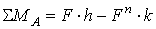Пр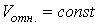и и 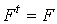получим 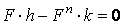, т.е.

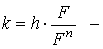коэффициент трения качения, измеряемый в единицах длины.

Часто используется величина 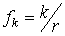, называемая приведённым коэффициентом трения качения. При этом сила трения качения 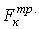по аналогии с силой трения скольжения может быть представлена в виде: .

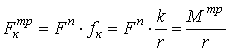
рис. 94

Мощность, затрачиваемая на трение, равна:

,

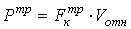где 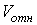- скорость качения центра катка.

Для подшипников качения: ,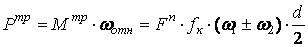

где d – диаметр подшипника по внутреннему кольцу.

Коэффициент 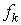принимается:

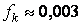- для шарикоподшипников;

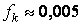- для роликоподшипников.