10. Уравновешивание масс в механизмах и машинах
10.1. Действие сил на фундамент. Условия уравновешивания
В общем случае в кинематических парах механизмов и машин возникают динамические усилия, переменные по величине и направлению. Через стойку они передаются на фундамент, вызывая дополнительные напряжения в отдельных звеньях, вибрацию и ухудшение условий работы. Чтобы этого избежать, необходимо рационально подобрать и расположить массы звеньев с условием полного или частичного гашения динамических усилий. Эта задача решается при уравновешивании.
Основными динамическими составляющими при работе любого механизма являются силы инерции, которые, как правило, переменны по величине и направлению. Это характерно и для случаев, когда входное звено вращается с постоянной угловой скоростью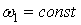 
(рис. 96). Все силы и моменты сил инерции можно привести к главному вектору и моменту относительно выбранной точки:
; 
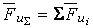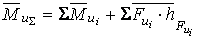
Полностью уравновешенным считается механизм, в котором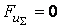 
и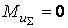 
, т.е. сила давления стойки на фундамент остаётся постоянной при движении звеньев.
Из теоретической механики известно, что: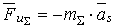 
,
где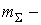 
масса всех подвижных звеньев; 
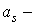ускорение центра масс системы.
Следовательно, для выполнения условия 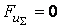необходимо, чтобы 
.
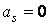Это равносильно требованию постоянства положения центра масс механизма относительно стойки. Такое уравновешивание называется статическим или уравновешиванием первого рода. В этом случае используется метод заменяющих (сосредоточенных) масс, обладающих массой, центром масс и моментом инерции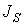 
заменяемого твёрдого тела (звена) с распределённой массой. Если поместить начало системы координат в центр масс системы, то условия эквивалентности заменяемой и заменяющих масс запишутся так:
; 
; 
; 
,
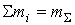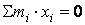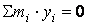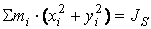т.е. в общем случае плоского звена необходимы четыре заменяющих массы. В частных случаях число заменяющих масс может быть сведено к двум. Например, для звена АВ (рис. 97) можно ограничиться частичной заменой его массы m дву-
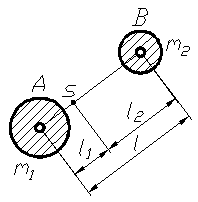мя массами m1 и m2, учитывая условия:
; 
.
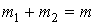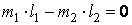Отсюда: 
; 
.
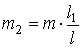Для полного уравновешивания механизма необходимо выполнение обоих условий: 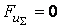; 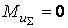, причём выполнение условия 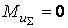решается при моментном (динамическом) уравновешивании, которое называется уравновешиванием второго рода.
рис. 97